pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 31 sampai dengan nomor 35 tentang:
- persamaan trigonometri,
- penerapan trigonometri,
- penafsiran data [statistika],
- ukuran pemusatan [median – statistika], dan
- ukuran penyebaran [varians – statistika].
Soal No. 31 tentang Persamaan Trigonometri
A. {120°, 180°}
B. {150°, 260°}
C. {180°, 270°}
D. {200°, 320°}
E. {210°, 330°}
Pembahasan
Langkah pertama untuk menyelesaikan soal persamaan trigonometri di atas adalah memindah ruas bilangan yang tidak mengandung variabel x ke ruas kanan.
1 + 2 sin x = 0
2 sin x = −1
sin x = −1/2
sin x yang bernilai negatif berada di kuadran III dan IV.
sin x = −1/2
sin x = sin(180° + 30°) [kuadran III]
x = 180°+30°
= 210°
sin x = sin(360° − 30°) [kuadran IV]
x = 360° − 30°
= 330°
Jadi, himpunan penyelesaian dari persamaan trigonometri di atas adalah {210°, 330°} (E).
Soal No. 32 tentang Penerapan Trigonometri
A. 800 m
B. 400√3 m
C. 400√2 m
D. 400/3 √2 m
E. 200 m

Pembahasan
Gambar ilustrasi untuk soal di atas adalah:

Tinggi menara merupakan sisi segitiga yang berada di depan sudut. Sedangkan jarak kaki menara terhadap pengamat merupakan sisi segitiga di samping sudut.
Hubungan antara sisi depan sudut dengan sisi samping sudut (desa) adalah fungsi tangens.

Jadi, tinggi menara tersebut adalah 400√3 m (B).
Soal No. 33 tentang Penafsiran Data [Statistika]
| Nilai | Jumlah Siswa |
| 50 60 70 80 90 100 |
5 15 10 12 6 2 |
Siswa yang lulus dan dapat diterima adalah mereka yang mendapat nila minimal 70. Persentase siswa yang tidak diterima adalah ….
A. 20%
B. 35%
C. 40%
D. 50%
E. 60%
Pembahasan
Perhatikan analisis tabel berikut ini!

Berdasarkan analisis tabel di atas, siswa yang tidak diterima sebanyak 20 siswa dari 50 pendaftar. Sehingga persentase yang tidak diterima adalah:
20/50 × 100% = 40%
Jadi, persentase siswa yang tidak diterima adalah 40% (C).
Soal No. 34 tentang Ukuran Pemusatan [Median – Statistika]
Median dari nilai lomba matematika tersebut adalah ….
A. 51,0
B. 51,5
C. 52,0
D. 52,5
E. 53,0
Pembahasan
Median adalah nilai data yang terletak di tengah. Untuk itu, kita hitung dulu jumlah semua datanya.
N = 3 + 7 + 10 + 12 + 11 + 6 + 1
= 50
1/2 N = 25
Berarti median data tersebut terletak pada data yang ke-25. Perhatikan analis histogram berikut!

Median data tersebut dapat ditentukan dengan rumus:
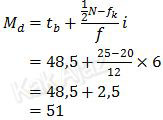
Jadi, median dari nilai lomba matematika tersebut adalah 51,0 (A).
Soal No. 35 tentang Ukuran Penyebaran [Varians – Statistika]
A. 0
B. 12/8
C. 14/8
D. 18/8
E. 28/8
Pembahasan
Ragam atau varians (s2) untuk data tunggal dirumuskan sebagai:

Untuk itu, kita cari dulu jumlah data (n) dan rata-ratanya.

Untuk memanfaatkan rumus varians di atas, sebaiknya dibuat tabel sebagai berikut:

Dengan demikian, varians data tersebut adalah:
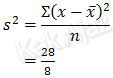
Jadi, jadi varians data tunggal tersebut adalah 28/8 (E).
Simak Pembahasan Soal Matematika IPS UN 2017 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
