pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 6 sampai dengan nomor 10 tentang:
- sistem pertidaksamaan linear,
- program linear,
- fungsi,
- komposisi fungsi, dan
- daerah asal komposisi fungsi.
Soal No. 6 tentang Sistem Pertidaksamaan Linear

Nilai maksimum fungsi objektif f(x, y) = 6x + 10y adalah ….
A. 46
B. 40
C. 34
D. 30
E. 24
Pembahasan
Karena koefisien x dan y pada fungsi objektif mempunyai nilai yang hampir sama besar, nilai maksimum fungsi objektif tersebut terletak pada titik potong kedua garis.
Garis yang melalui titik (0, 5) dan (5, 0).
5x + 5y = 5 × 5
x + y = 5 … (1)
Garis yang melalui titik (0, 2) dan (−1, 0).
2x − y = 2×(−1)
2x − y = −2 … (2)
Titik potong kedua garis dapat dicari dengan melakukan eliminasi persamaan (1) dan (2).
x + y = 5
2x − y = −2
⎯⎯⎯⎯⎯⎯⎯ +
3x = 3
x = 1
Eliminasi x = 1 ke persamaan (1) diperoleh:
1 + y = 5
y = 4
Dengan demikian, nilai maksimum tercapai saat x = 1 dan y = 4.
f(x, y) = 6x + 10y
f(1, 4) = 6×1+10×4
= 6 + 40
= 46
Jadi, nilai maksimum fungsi objektif f(x, y) = 6x + 10y adalah 46 (A).
Soal No. 7 tentang Program Linear
A. Rp25.000.000.000,00
B. Rp26.250.000.000,00
C. Rp26.600.000.000,00
D. Rp26.670.000.000,00
E. Rp31.250.000.000,00
Pembahasan
Tabel bantuan untuk soal di atas adalah:

Berdasarkan tabel di atas, diperoleh persamaan:
x + y = 125 … (1)
4x + 3y = 400 … (2)
f(x, y) = 250.000.000x + 200.000.000y
Eliminasi persamaan (1) dan (2).

Substitusi y = 100 ke persamaan (1) diperoleh:
x + 100 = 125
x = 25
Dengan demikian, nilai fungsi objektifnya adalah:
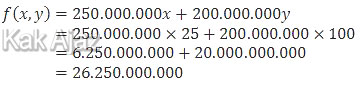
Jadi, penghasilan maksimum yang dapat diperoleh pengusaha perumahan tersebut adalah Rp26.250.000.000,00 (B).
Soal No. 8 tentang Fungsi
A. {y│−4 ≤ y ≤ 0, y ∈ R}
B. {y│−4 ≤ y ≤ 11, y ∈ R}
C. {y│−4 ≤ y ≤ 5, y ∈ R}
D. {y│0 ≤ y ≤ 5, y ∈ R}
E. {y│0 ≤ y ≤ 11, y ∈ R}

Pembahasan
Untuk menentukan daerah hasil, cukup dengan memasukkan batas daerah asal dan sumbu simetri ke persamaan fungsi y.
Sumbu simetri fungsi y = x2 − 2x − 3 adalah:
x = −b/2a
= −(−2)/(2×1)
= 1
Sedangkan batas daerah asalnya adalah:
−1 ≤ x ≤ 4
Nah, sekarang kita substitusikan x = 1, x = −1, dan x = 4 ke fungsi y = f(x).
f(x) = x2 − 2x − 3
f(1) = 12 − 2×1 − 3 = −4 [minimum]
f(−1) = (−1)2 − 2×(−1) − 3 = 0
f(4) = 42 − 2×4 − 3 = 5 [maksimum]
Berdasarkan hasil substitusi di atas, nilai terendahnya adalah −4 dan tertingginya adalah 5. Dengan demikian, daerah hasilnya adalah:
−4 ≤ y ≤ 5
Jadi, daerah hasil fungsi tersebut adalah opsi (C).
Soal No. 9 tentang Komposisi Fungsi
A. 4x2 − 14x + 7
B. 4x2 − 10x + 7
C. 4x2 − 10x + 5
D. 4x2 + 2x − 11
E. 4x2 + 2x + 7
Pembahasan
Fungsi komposisi (f ∘ g)(x) bisa ditulis f[g(x)] yang berarti fungsi g(x) dimasukkan ke fungsi f(x).
f(x) = x2 + x + 1
f[g(x)] = g2(x) + g(x) +1
= (2x − 3)2 + (2x − 3 )+ 1
= 4x2 − 12x + 9 + 2x − 3 + 1
= 4x2 − 10x + 7
Jadi, fungsi komposisi (f ∘ g)(x) adalah opsi (B).
Soal No. 10 tentang Daerah Asal Komposisi Fungsi
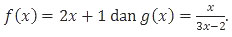
Daerah asal fungsi komposisi (g∘f)(x) adalah ….
A. {x│x ≠ −1/6, x ∈ R}
B. {x│x ≠ −1/2, x ∈ R}
C. {x│x ≠ 1/6, x ∈ R}
D. {x│x ≠ 2/3, x ∈ R}
E. {x│x ∈ R}
Pembahasan
Komposisi fungsi (g ∘ f)(x) = g[f(x)].
![Komposisi fungsi (g ∘ f)(x) = g[f(x)] Komposisi fungsi (g ∘ f)(x) = g[f(x)]](https://1.bp.blogspot.com/-I4j8mnkRISE/XZt4jx8QFjI/AAAAAAAAPeM/rdJ3giowzB8BCAQKdFygq_BngeMxyTOXQCLcBGAsYHQ/s1600/Komposisi-gof.jpg)
Ternyata fungsi g[f(x)] berbentuk pecahan. Agar memenuhi syarat daerah asal, penyebut pecahan tersebut tidak boleh sama dengan nol.
6x + 1 ≠ 0
6x ≠ −1
x ≠ −1/6
Jadi, daerah asal fungsi komposisi (g ∘ f)(x) adalah opsi (A).
Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
