pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 21 sampai dengan nomor 25 tentang:
- turunan fungsi,
- aplikasi turunan,
- integral,
- segitiga trigonometri, dan
- kuadran trigonometri.
Soal No. 21 tentang Turunan Fungsi
A. f’(x) = 12x2 − 4x − 24
B. f’(x) = 12x2 − 8x + 24
C. f’(x) = 24x − 8
D. f’(x) = 12x2 − 16x + 24
E. f’(x) = 12x2 − 8x − 24
Pembahasan
Sebelum diturunkan, dikalikan dulu saja supaya tidak menurunkan dalam bentuk u∙v.
f(x) = (4x2 − 12x)(x + 2)
= (4x2 − 12x)x + (4x2 − 12x)2
= 4x3 − 12x2 + 8x2 − 24x
= 4x3 − 4x2 − 24x
f’(x) = 4∙3x2 − 4∙2x1 − 24∙1x
= 12x2 − 8x − 24
Jadi, turunan pertama fungsi tersebut adalah opsi (E).
Soal No. 22 tentang Aplikasi Turunan
A. −2< x <3
B. −3 < x < 2
C. x < 2 atau x > 3
D. x < −3 atau x > 2
E. x < −2 atau x > 3
Pembahasan
Agar suatu fungsi naik maka turunan fungsi tersebut harus lebih dari nol.
f(x) = x3 + 3/2 x2 − 18x + 5
f’(x) > 0
3x2 + 3x − 18 > 0
x2 + x − 6 > 0
(x + 3)(x − 2) > 0
Pembuat nol: x = −3 dan x = 2
Karena tanda pertidaksamaannya “>” maka intervalnya berada di sebelah kiri −3 dan di sebelah kanan 2.
x < −3 atau x > 2
Jadi, grafik fungsi tersebut naik pada interval x < −3 atau x > 2 (D).
Soal No. 23 tentang Integral
A. ½ x4 − 6x3 + 2x2 − 5x + C
B. ½ x4 − 6x3 + x2 − 5x + C
C. ½ x4 − 3x3 + x2 − 5x + C
D. ½ x4 − 3x3 + 2x2 − 5x + C
E. ½ x4 − 6x3 − 2x2 − 5x + C

Pembahasan
Soal ini Cuma butuh kecermatan dan ketelitian. Mari kita kerjakan secara hati-hati.
∫ (2x3 − 9x2 + 4x − 5) dx
= 2 ∙ ¼ x4 − 9 ∙ ⅓ x3 + 4 ∙ ½ x2 − 5x + C
= ½ x4 − 3x3 + 2x2 − 5x + C
Jadi, hasil dari integral tersebut adalah opsi (D).
Soal No. 24 tentang Segitiga Trigonometri
A. 3/20 √10
B. 7/20 √10
C. 2/3 √10
D. 3/2 √10
E. 7/3 √10
Pembahasan
Perhatikan gambar di bawah ini!

Panjang AB dapat dicari melalui rumus Pythagoras sebagai berikut:
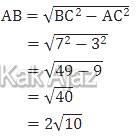
Nilai tan C merupakan perbandingan antara AB terhadap AC.

Jadi, nilai tan C adalah 2/3 √10 (C).
Soal No. 25 tentang Kuadran Trigonometri
A. √3 − 1
B. √3 + 1
C. 0
D. 1
E. 2
Pembahasan
Untuk menyelesaikan soal ini, harus mengingat kembali nilai trigonometri di berbagai kuadran.

Jadi, nilai dari cos 300° +sin 150° − tan 135° adalah 2 (E).
Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
