Pembahasan Pengetahuan Kuantitatif No. 71

Pembahasan soal Pengetahuan Kuantitatif Tes Potensi Skolastik (TPS) pada Ujian Tulis Berbasis Komputer (UTBK) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2019 nomor 71 sampai dengan nomor 80 tentang pengetahuan kuantitatif.

Soal No. 71

Pembahasan

Rata-rata gaji pegawai bengkel tersebut adalah:

Jadi, rata-rata gaji ketujuh pegawai tersebut berkisar pada Rp169.000.000,00 (C).

Soal No. 72

Pembahasan

Jumlah suatu himpunan bilangan adalah 465.

N = 465

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup (A).

Soal No. 73

Tabel berikut menunjukkan banyaknya CD terjual pada suatu toko selama suatu periode. Jika baris atas menunjukkan jumlah CD terjual per hari dan baris bawah menunjukkan jumlah hari di mana CD terjual, maka berapa median dari CD terjual selama periode itu.

Pembahasan

Kita urutkan data pada tabel di atas berdasarkan jumlah CD yang terjual setiap harinya.

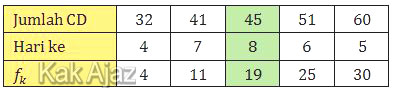
Maksud tabel di atas adalah: 4 hari pertama, setiap harinya terjual 32 CD. 7 hari berikutnya, setiap hari terjual 41 CD, dan seterusnya.

Periode penjualan CD tersebut adalah 30 hari. Sehingga median terletak pada hari ke-15 dan ke-16. Pada kedua hari tersebut jumlah CD yang terjual adalah 45.

Jadi, median dari CD terjual selama periode itu adalah 45 (C).

Soal No. 74

Pembahasan

Dua pernyataan di atas tidak bisa menghasilkan nilai modus, kecuali jika digunakan secara bersama-sama sebagai berikut:

3 bilangan mempunyai rata-rata = 4 dan modus = 4, maka ketiga bilangan tersebut masing-masing pasti = 4, sehingga nilai median juga = 4.

4, 4, 4

Jadi, DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup (C).

Soal No. 75

Pembahasan

Misal A adalah himpunan bilangan prima berdigit tunggal.

A = {2, 3, 5, 7}

Faktorisasi prima dari 84 bisa kita cari melalui pohon faktor berikut.

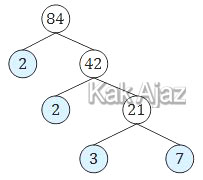
Misal B adalah himpunan faktorisasi prima dari 84.

B = {2, 2, 3, 7}

Suatu himpunan bilangan dibangun dengan menggunakan bilangan di atas, misal C.

C = {2, 2, 2, 3, 3, 5, 7, 7}

Modus himpunan C (bilangan pada himpunan C yang sering muncul) dari adalah 2.

Jadi, modus data di atas adalah 2 (B).

Soal No. 76

Pada gambar berikut, berapakah nilai dari z?

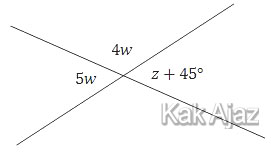
Pembahasan

Perhatikan gambar di bawah ini!

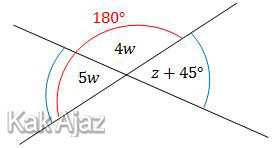
Sudut 5w dan sudut 4w berpelurus, jumlahnya 180°.

Sedangkan sudut (z + 45°) dan sudut 5w besarnya sama.

Jadi, nilai dari z adalah 55° (C).

Soal No. 77

Pada gambar berikut, l∥m. Berapakah nilai dari x?

1)	x = 3y
2)	y = 180° − x

A.	Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B.	Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C.	DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D.	Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E.	Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

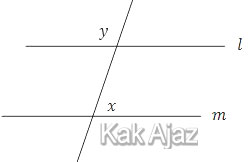
Pembahasan

Perhatikan gambar berikut!

Sudut x dan sudut y berpelurus, sehingga:

x + y = 180° … (1)

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup (A).

Soal No. 78

Jika PQ = PR, berapakah luas segitiga PQR?

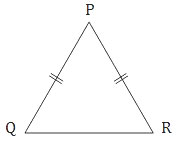
1)	Sudut PQR = 60°
2)	QR = 10

A.	Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B.	Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C.	DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D.	Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E.	Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Artkel Terkait  soal tryout II utbk sbmptn 2020 fisika dan pembahasan

Pembahasan

1)	Sudut PQR = 60° 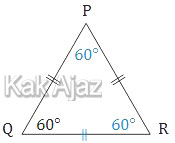Ternyata PQR adalah segitiga sama sisi. Namun pernyataan (1) saja tidak bisa digunakan untuk menentukan luas segitiga.
2)	QR = 10  Pernyataan (2) juga tidak bisa digunakan untuk menentukan luas segitiga.

Jika pernyataan (1) dan (2) digunakan bersama, maka diperoleh segitiga PQR adalah segitiga sama sisi dengan panjang sisi 10. Sehingga luas segitiga bisa dicari.

Jadi, DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup (C).

Soal No.79

Pembahasan

Misal a = 4 dan b = 10 maka sisi ketiga, yaitu c, harus memenuhi:

Nilai c harus berada di antara 6 dan 14. Yang memenuhi hanya 12 [pernyataan 2].

Jadi, panjang sisi ketiga adalah opsi (B).

Soal No. 80

Pembahasan

Persegi panjang R dan S mempunyai luas yang sama.

Jadi, lebar lukisan S adalah 3 kaki (B).

Simak Pembahasan Soal TPS UTBK SBMPTN 2019 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih