pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 1 sampai dengan nomor 5 paket 2 tentang:
- fungsi kuadrat,
- sistem persamaan linear,
- sistem pertidaksamaan linear [daerah sistem pertidaksamaan],
- sistem pertidaksamaan linear [model matematika], dan
- program linear.
Soal No. 1 tentang Fungsi Kuadrat

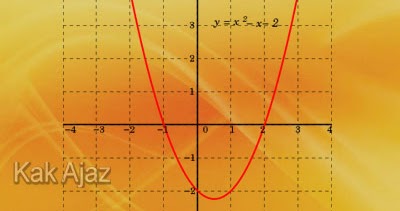
Jika grafik fungsi f(x) = ax2 + bx + c seperti pada gambar, nilai a, b, dan c yang memenuhi adalah ….
| A. | a > 0, b > 0, dan c > 0 |
| B. | a < 0, b > 0, dan c > 0 |
| C. | a < 0, b > 0, dan c < 0 |
| D. | a > 0, b < 0, dan c > 0 |
| E. | a < 0, b < 0, dan c < 0 |
Pembahasan
Ketentuan nilai a, b, dan c pada grafik fungsi kuadrat adalah sebagai berikut:
| a > 0 | : | grafik terbuka ke atas |
| a < 0 | : | grafik terbuka ke bawah |
| ab > 0 | : | sumbu simetri sebelah kiri |
| ab < 0 | : | sumbu simetri sebelah kanan |
| c > 0 | : | memotong sumbu y positif |
| c < 0 | : | memotong sumbu y negatif |
Berdasarkan ketentuan di tersebut, grafik di atas adalah:
| terbuka ke atas | : | a > 0 |
| simetri sebelah kiri | : | b > 0 [a > 0] |
| memotong sumbu y positif | : | c > 0 |
Jadi, nilai a, b, dan c yang sesuai dengan grafik di atas adalah opsi (A).
Perdalam materi ini di Pembahasan Matematika UN: Fungsi Kuadrat.
Soal No. 2 tentang Sistem Persamaan Linear
| A. | Rp19.000,00 |
| B. | Rp23.000,00 |
| C. | Rp25.000,00 |
| D. | Rp27.000,00 |
| E. | Rp30.000,00 |
Pembahasan
Harga 3 buah buku dan 2 buah penggaris Rp18.000,00.
3x + 2y = 18.000 … (1)
Harga sebuah buku Rp1.000,00 lebih mahal dari sebuah penggaris.
x = y + 1.000 … (2)
Substitusi persamaan (2) dan (1) diperoleh:
| 3(y + 1.000) + 2y | = | 18.000 |
| 3y + 3000 + 2y | = | 18.000 |
| 5y | = | 15.000 |
| y | = | 3.000 |
Substitusi persamaan y = 3.000 ke persamaan (2) diperoleh:
Dengan demikian, harga 2 buah buku dan 5 buah penggaris adalah:
| 2x + 5y | = | 2 × 4.000 + 5 × 3.000 |
| = | 8.000 + 15.000 | |
| = | 23.000 |
Jadi, harga 2 buah buku dan 5 buah penggaris adalah Rp23.000,00 (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Sistem Persamaan Linear.
Soal No. 3 tentang Sistem Pertidaksamaan Linear
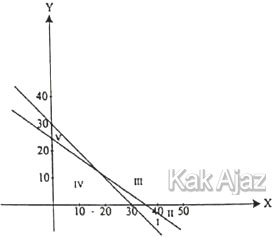

Pembahasan
Kedua pertidaksamaan di atas bertanda “≤” sehingga dapat dipastikan daerah pertidaksamaan keduanya berada di bawah garis.
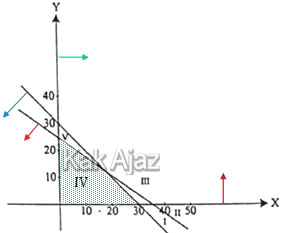
Sementara itu, sistem pertidaksamaan tersebut berada di kuadran pertama (x ≥ 0, y ≥ 0).
Jadi, daerah yang memenuhi sistem pertidaksamaan linear tersebut adalah daerah IV (D).
Perdalam materi ini di Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan].
Soal No. 4 tentang Sistem Pertidaksamaan Linear
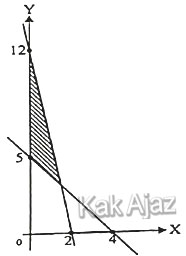
| A. | 6x + y ≤ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0 |
| B. | 6x + y ≥ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0 |
| C. | 6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0 |
| D. | 6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0 |
| E. | x + 6y ≤ 12; 4x + 5y ≥ 20; x ≥ 0; y ≥ 0 |
Pembahasan
Untuk menentukan persamaan garis dari suatu grafik, gunakan konsep berikut ini!

Berdasarkan konsep di atas, persamaan garis pada grafik di bawah ini adalah:
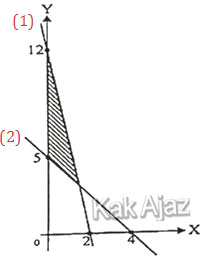
(1) 12x + 2y = 24
(2) 5x + 4y = 20
Persamaan garis (1) perlu disederhanakan, sedangkan persamaan (2) sudah dalam bentuk yang paling sederhana. Sehingga,
(1) 6x + y = 12
(2) 5x + 4y = 20
Daerah yang diarsir terletak di sebelah kiri garis (1) dan di atas garis (2). Tanda pertidaksamaan untuk daerah sebelah kiri adalah “≤” sedangkan daerah atas adalah “≥” . Diperoleh:
(1) 6x + y ≤ 12
(2) 5x + 4y ≥ 20
Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.
x ≥ 0; y ≥ 0
Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (A).
Perdalam materi ini di Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan].
Soal No. 5 tentang Program Linear
| A. | Rp1.200.000.000,00 |
| B. | Rp920.000.000,00 |
| C. | Rp840.000.000,00 |
| D. | Rp800.000.000,00 |
| E. | Rp795.000.000,00 |
Pembahasan
Berikut ini adalah tabel bantuan untuk soal program linear di atas.

Berdasarkan tabel bantuan di atas, model matematikanya adalah:
4x + 8y ≤ 80.000
4x + 5y ≤ 53.000
Untuk menyelesaikannya, kita ubah ke persamaan kemudian kita eliminasi.
| 4x + 8y | = | 80.000 |
| 4x + 5y | = | 53.000 |
| ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ | ||
| 3y | = | 27.000 |
| y | = | 9.000 |
Substitusi y = 90.000 ke persamaan pertama diperoleh:
| 4x + 8 × 9.000 | = | 80.000 |
| 4x | = | 80.000 − 72.000 |
| 4x | = | 8.000 |
| x | = | 2.000 |
Sementara itu, fungsi sasaran program linear tersebut adalah:
z = 60.000x + 80.000y
Sehingga nilainya adalah:
| z | = | 60.000 × 2.000 + 80.000 × 9.000 |
| = | 120.000.000 + 720.000.000 | |
| = | 840.000.000 |
Jadi, keuntungan maksimum petani tersebut adalah Rp840.000.000,00 (C).
Perdalam materi ini di Pembahasan Matematika UN: Program Linear.
Simak Pembahasan Soal Matematika IPA UN 2019 Paket 2 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat