pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 11 sampai dengan nomor 15 paket 2 tentang:
- invers fungsi,
- matriks,
- transformasi geometri,
- turunan fungsi, dan
- limit fungsi.
Soal No. 11 tentang Invers Fungsi
| A. | 4/3 |
| B. | 2/3 |
| C. | 1/3 |
| D. | −2/3 |
| E. | −4/3 |
Pembahasan
Menentukan invers fungsi atau fungsi kebalikan dapat dilakukan dengan cara meletakkan variabel x di ruas kiri terlebih dahulu.
| f(x) | = | √(3x + 5) |
| y | = | √(3x + 5) |
| y2 | = | 3x + 5 |
| 3x | = | y2 − 5 |
| x | = | ⅓ (y2 − 5) |
Kemudian x di ruas kiri kita ubah menjadi f−1(x) sedangkan y di ruas kanan kita ubah menjadi x.
f−1(x) = ⅓ (x2 − 5)
Nah, sekarang tinggal memasukkan nilai x = 3.
| f−1(3) | = | ⅓ (32 − 5) |
| = | ⅓ ⋅ 4 | |
| = | 4/3 |
Jadi, nilai dari f−1(3) adalah 4/3 (A).
Perdalam materi ini di Pembahasan Matematika UN: Komposisi dan Invers Fungsi.
Soal No. 12 tentang Matriks

Nilai 2a − b = ⋯.
Pembahasan
Kita operasikan dulu perkalian matriks di ruas kiri.

Diperoleh persamaan linear:
2a + 4b = 8 … (1)
a − 2b = 12 … (2)
Persamaan (1) kita bagi 2 kemudian kita eliminasikan dengan persamaan (2).
| a + 2b | = | 4 | |
| a − 2b | = | 12 | |
|
|
+ | ||
| 2a | = | 16 | |
| a | = | 8 | |
Substitusi a = 8 ke persamaan (1) diperoleh:
Dengan demikian,
| 2a − b | = | 2×8 − (−2) |
| = | 16 + 2 | |
| = | 18 |
Jadi, nilai dari 2a − b adalah 18 (A).
Perdalam materi ini di Pembahasan Matematika UN: Matriks.
Soal No. 13 tentang Transformasi Geometri
| A. | (−1, 1) |
| B. | (1, 1) |
| C. | (1, 3) |
| D. | (2, −3) |
| E. | (2, 3) |

Pembahasan
Matriks transformasi X berordo 2×2, misal
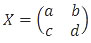
Bayangan A oleh transformasi X berlaku hubungan
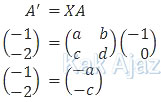
Sehingga diperoleh:
a = 1
c = 2
Demikian juga bayangan B oleh transformasi X berlaku hubungan
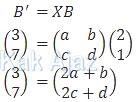
Sehingga diperoleh:
2a + b = 3
2c + d =7
Substitusi a = 1 dan c = 2 pada kedua persamaan di atas diperoleh:
Dengan demikian matriks transformasi X adalah:
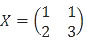
Sedangkan invers matriks transformasi X adalah:
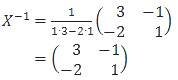
Untuk menentukan titik C dari C’ berlaku hubungan:
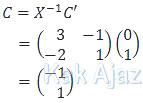
Jadi, titik C adalah (−1, 1) (A).
Perdalam materi ini di Pembahasan Matematika UN: Transformasi Geometri.
Soal No. 14 tentang Turunan Fungsi
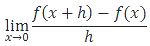
adalah ….
| A. | 2x − 3 |
| B. | 4x − 3 |
| C. | 6x − 3 |
| D. | 4x3 − 3x2 |
| E. | 4x3 − 2x |
Pembahasan
Perhatikan rumus di bawah ini!

Dengan demikian hasil limit fungsi tersebut adalah turunan dari fungsi f(x).
f(x) = 2x2 − 3x − 5
f’(x) = 4x − 3
Jadi, hasil dari limit tersebut adalah 4x − 3 (B).
Perdalam materi ini di Pembahasan Matematika UN: Turunan Fungsi.
Soal No. 15 tentang Limit Fungsi

| A. | |
| B. | 25/9 |
| C. | 25/6 |
| D. | 25/3 |
| E. | ∞ |
Pembahasan
Limit fungsi di atas lebih mudah dikerjakan dengan menggunakan dalil L’Hopital, caranya hanya dengan menurunkan pembilang dan penyebutnya. Misalkan pembilangnya adalah f(x) dan penyebutnya g(x).
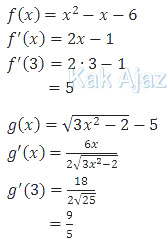
Dengan demikian,
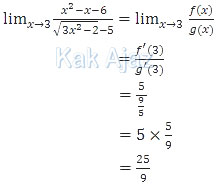
Jadi, nilai dari limit di atas adalah 25/9 (B).
Perdalam materi ini di Pembahasan Matematika UN: Limit Fungsi.
Simak Pembahasan Soal Matematika IPA UN 2019 Paket 2 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
