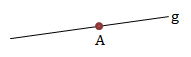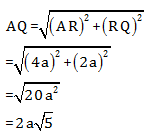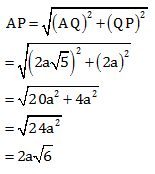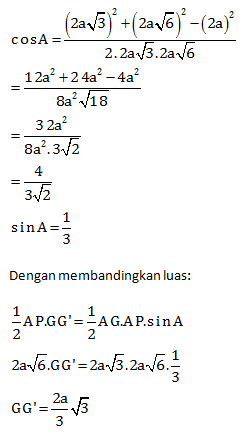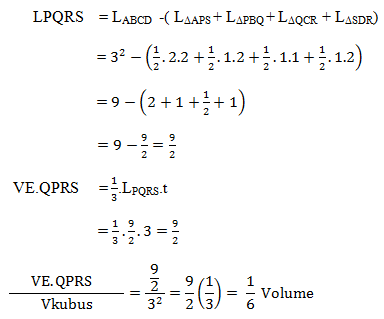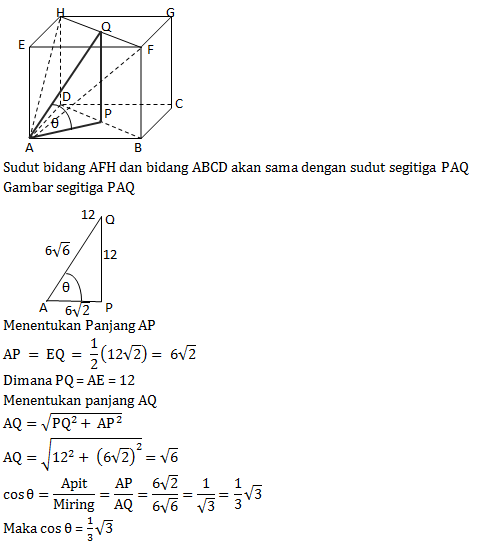Untuk Pembelajaran selanjutnya…
Hey..hey kamu kelas XII yang baru naik tingkat. Gimana rasanya jadi anak paling gede di sekolah. Di matematika bab pertama yang kamu pelajari di matematika wajib yaitu dimensi tiga. Disini kita kasih rangkuman materinya, bagian-bagian materi yang wajib kamu kuasai di bab ini. Bukan hanya rangkuman disini juga kamu bisa simak video pembelajaran mengenai dimensi tiga ada 9 part. Lengkap banget. Ga usah bayar-bayar. Gratis buat kalian. Untuk penguasan yang lebih mendalam kita kasih 20 contoh soal & jawaban berikut pembahasannya lengkap! Ok, bagian-bagianya bisa dilihat di daftar isi yah.
Kedudukan Titik, Garis, dan Bidang dalam Ruang
- Titik, ditentukan dari letaknya dan tidak memiliki ukuran digambarkan dengan memakai tanda noktah kemudian dibubuhi dengan nama titik itu.

- Garis, hanya memiliki ukuran panjang tidak memiliki ukuran lebar. Sebuah garis bisa dilukiskan sebagian saja disebut wakil garis.

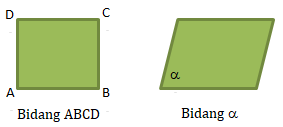
- Bidang, dapat digambarkan sebagian saja disebut wakil bidang. Wakil bidang memiliki panjang dan lebar yang dapat berbentuk persegi atau bujur sangkar, persegi panjang, atau jajar genjang. Nama wakil bidang dituliskan di daerah pojok bidang
Kedudukan Titik Terhadap Garis dan Titik Terhadap Bidang
Kedudukan titik terhadap garis
Kedudukan titik terhadap bidang
Kedudukan garis terhadap garis dan garis terhadap bidang
Kedudukan garis terhadap garis lain
- Dua garis berpotongan

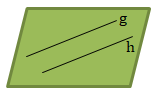
- Dua garis sejajar
- Dua garis berimpit

- Dua garis bersilangan
Garis g menembus bidang di titik A, titik A tidak terletak pada garis h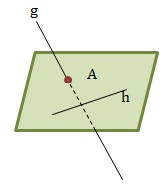
Videonya ada 9 part ya. Kalau terlalu kecil tekan opsi full screen di pojok kanan video. Silahkan menyimak!
- Part 1
- Part 2
- Part 3
- Part 4
- Part 5
- Part 6
- Part 7
- Part 8
- Part 9
Soal No.1 (UTBK 2019)
Misalkan balok ABCD.EFGH dengan AB = 2 cm, BC = 1 cm, dan AE = 1 cm. Jika P adalah titik tengah AB dan θ adalah ∠EPG, maka cos θ adalah….
Soal No.3 (SNMPTN 2011)
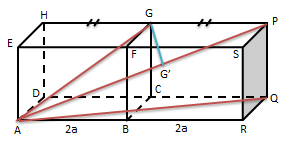
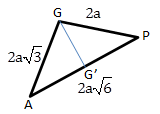
Diketahui kubus ABCD.EFGH dengan panjang rusuknya 2a. Jika titik P berada pada perpanjangan garis GH sehingga HG=GP maka jarak titik G ke garis AP adalah …
PEMBAHASAN :
Jika dibuat gambar sebagai berikut:
Menentukan panjang AQ
Menentukan panjang AP
Menentukan Panjang GG’ dengan cara membandingkan luas
Soal No.4 (UN 2008)
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H ke garis AC adalah … cm
PEMBAHASAN :
Jika dibuat gambarnya sebagai berikut:
Jawaban : C
Soal No.5 (Mat IPA SBMPTN 2013)
Diketahui kubus ABCD.EFGH mempunyai sisi 4cm. Titik P adalah titik tengah CD, titik Q adalah titik tengah EH, dan titik R adalah tengah BF. Jarak P ke QR adalah …
Soal No.4 (UN 2014)
Soal No.5 (SBMPTN 2014)
PEMBAHASAN :
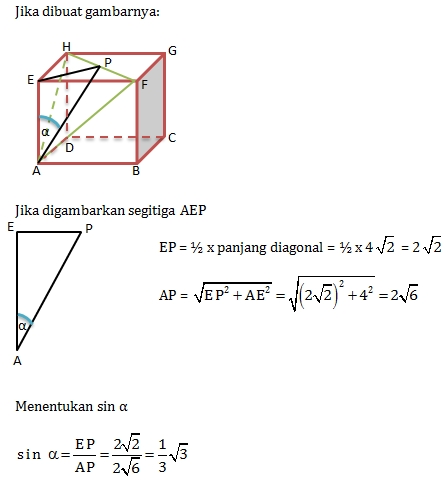
Jika Kubus ABCD.EFGH digambarkan sebagai berikut
Jika digambarkan limas E. PQRS
Menentukan perbandingan V limas E.PQRS dengan V Kubus
Jawaban : A
Soal No.6 (UN 2014)
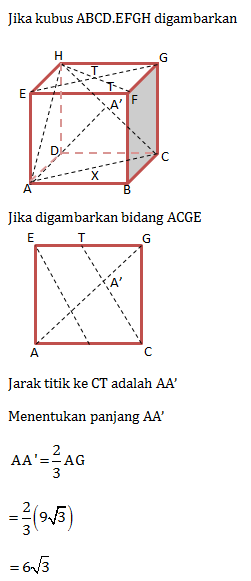
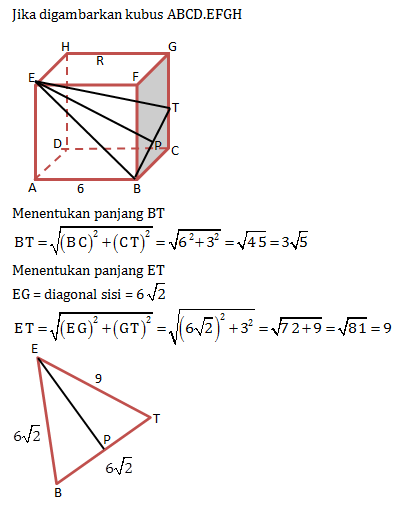
Diketahui kubus ABCD.EFGH dengan rusuk 9 cm. Jika titik T terletak pada pertengahan garis HF. Jarak titik A ke garis CT adalah …
Soal No.7 (SBMPTN 2014)
Diberikan balok ABCD.EFGH dengan AB = AE = 4 dan BC = 3. Titik P dan Q masing-masing titik tengah FG dan GH. Maka tangen sudut bidang diagonal FHDB dan bidang PQDB adalah….
PEMBAHASAN :
Jika digambarkan balok ABCD.EFGH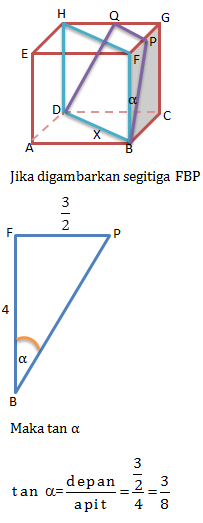
Jawaban : C
Soal No.8 (UN 2013)
Kubus ABCD.EFGH memiliki panjang rusuk 12 cm. Nilai kosinus sudut antara bidang AFH dan bidang ABCD adalah …
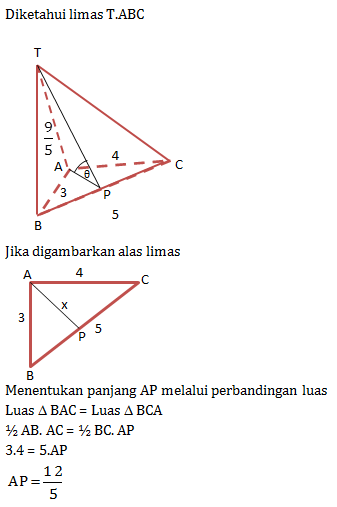
Soal No.9 (SBMPTN 2013)
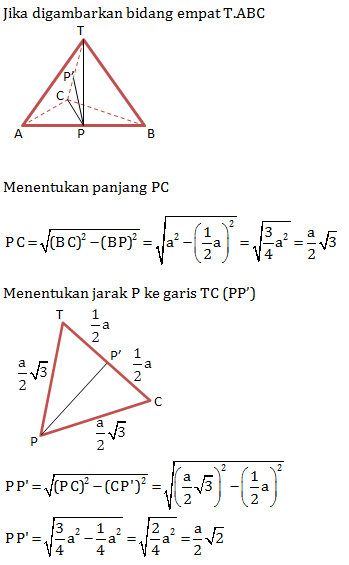
Diberikan bidang empat beraturan T.ABC dengan panjang rusuk a. Jika titik P adalah titik tengah rusuk AB maka jarak titil P ke garis TC adalah…
PEMBAHASAN :
Jawaban : C
Soal No.10 (UN 2013)
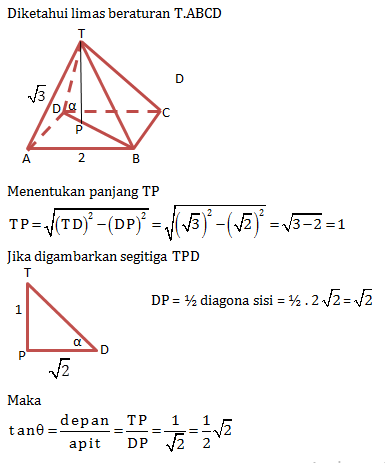
Diketahui limas beraturan T.ABCD dengan ABCD adalah persegi yang memiliki panjang AB = 4 cm dan TA = 6 cm. Jarak titik C ke garis AT adalah …
Soal No.11 (SBMPTN 2012)
Diberikan limas T.ABC dengan AB = AC = BC = 12 dan TA = TB = TC = 10. Jarak dari titik T ke bidang ABC adalah….
PEMBAHASAN :
Jawaban : A
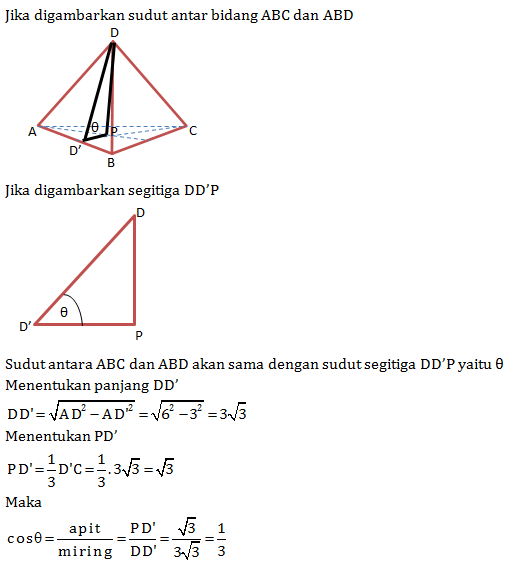
Soal No.12 (UN 2013)
Nilai kosinus sudut antara bidang ABC dan ABD dari gambar bidang empat beraturan berikut adalah …
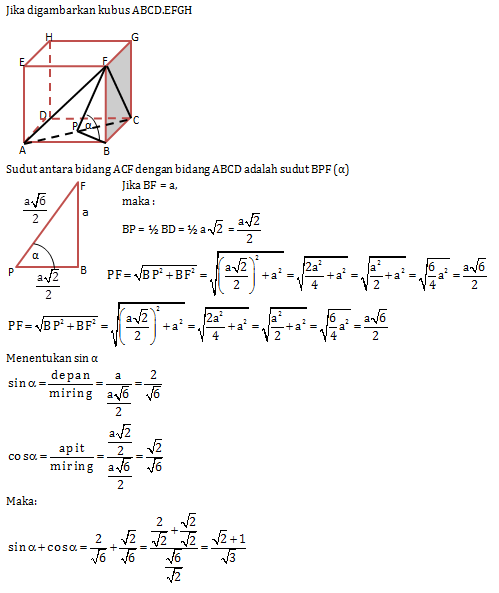
Soal No.13 (SBMPTN 2012)
Diberikan kubus ABCD.EFGH. Jika α adalah sudut antara bidang ACF dan bidang ABCD, maka sin α + cos α = …
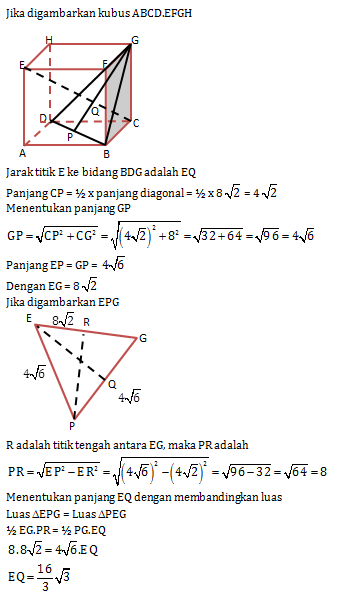
Soal No.14 (UN 2012)
Kubus ABCD.EFGH panjang rusuk 8 cm. Jarak titik E ke bidang BDG adalah…
Soal No.15 (SNMPTN 2011)
Soal No.16 (UN 2012)
Soal No.17 (SNMPTN 2010)
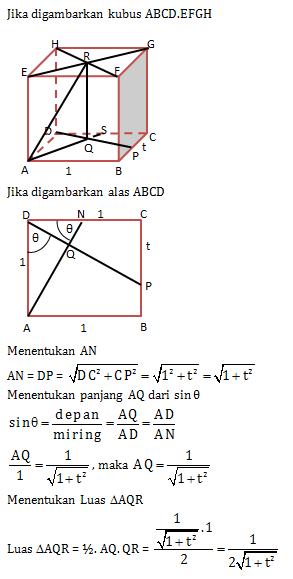
Kubus ABCD.EFGH panjang sisinya 1 dm. titik P pada BC fengan |PC| = t dm. Titik Q adalah proyeksi A pada DP dan R adalah proyeksi Q pada bidang EFGH. Luas segitiga AQR adalah…dm2
Soal No.18 (UN 2011)
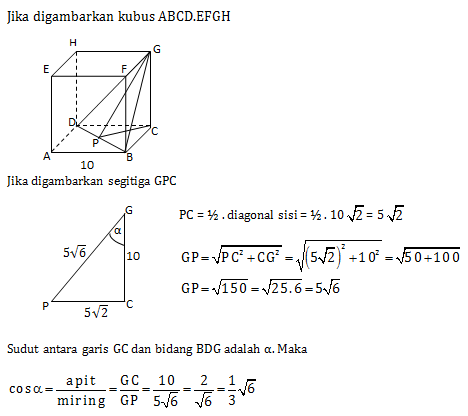
Diketahui kubus ABCD.EFGH dengan rusuk 10 cm. Kosinus sudut antara garis GC dan bidang BDG adalah…
Soal No.19 (SNMPTN 2008)
- 30o
- 45o
- 60o
- 75o
- 90o
Soal No.20 (UN 2010)
Diketahui kubus ABCD.EFGH dengan rusuk 6 cm dan T adalah titik tengah CG. Jarak titik E ke BT adalah…
Soal No.21 (UN 2010)
Diketahui kubus ABCD.EFGH dengan rusuk 8cm. Panjang proyeksi DE pada bidang BDHF adalah …
PEMBAHASAN :
Gambarkan kubus ABCD.EFGH seperti di bawah ini!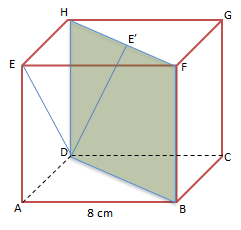
Diketahui:
Panjang rusuk = 8cm
proyeksi DE = DE’
Menentukan panjang proyeksi DE pada bidang BDHF dengan melihat segitiga DHE’ pada bidang BDHF:![]()
Jawaban : D
Soal No.22 (UN 2007)
Perhatikan gambar kubus di bawah ini!

Jarak bidang ACH dan bidang BEG adalah …
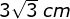
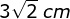
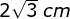
- 3 cm

PEMBAHASAN :
Diketahui:
Panjang rusuk = 6 cm
Panjang diagonal ruang = ![]()
Menentukan jarak bidang ACH dan bidang BEG
Gambarkan kubus ABCD.EFGH beserta bidang ACH dan bidang BEG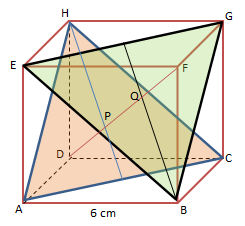

Jadi, jarak bidang ACH dan bidang BEG yaitu PQ![]()
Jawaban : C
Soal No.23 (UN 2003)
Pada gambar kubus ABCD.EFGH titik-titik K, L, dan M berturut-turut merupakan titik tengah BC, CD, dan CG. Jarak antara bidang AFH dengan bidang KLM adalah …
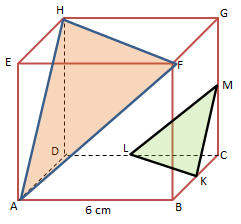
PEMBAHASAN :
Diketahui:
Panjang rusuk = 12 cm
Panjang diagonal ruang = ![]()
Menentukan jarak bidang AFH dengan bidang KLM
Gambarkan kubus ABCD.EFGH beserta bidang AFH dan bidang KLM
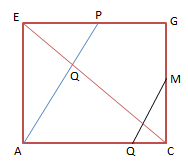
Berdasarkan gambar dapat diketahui bahwa jarak antara bidang AFH dengan bidang KLM adalah ST![]()
Jawaban : D
Soal No.24 (UN 2004)
- 5
- 6
- 7


PEMBAHASAN :
Diketahui:
Panjang AB = ![]()
Panjang AT = 10 cm
Titik tengah CT = P
Menentukan jarak P ke diagonal BD
Berdasarkan gambar di atas jarak titik P ke diagonal sisi BD adalah OP
Jawaban : A
Soal No.25 (UN 2003)
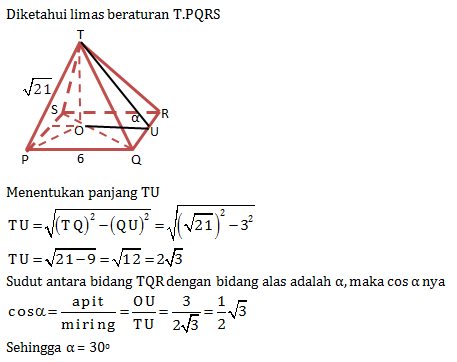
Perhatikan gambar limas beraturan T.ABCD, P, Q, R, dan S berturut-turut adalah titik tengah rusuk AB, AD, BC, dan CD. Nilai sinus sudut antara bidang TPQ dengan bidang TRS adalah …

PEMBAHASAN :
Diketahui:
Panjang rusuk = 12cm
Titik tengah AB = P
Titik tengah AD = Q
Titik tengah BC = R
Titik tengah CD = S
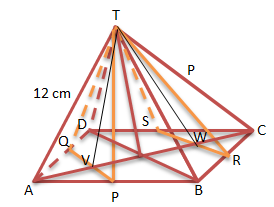
Menentukan sudut sinus antara bidang TPQ dan TRS (sudut VTW)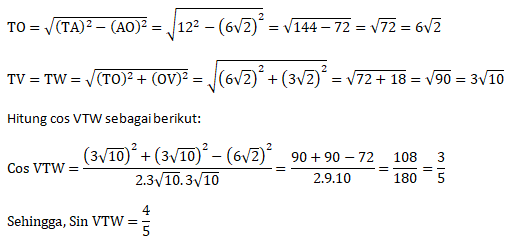
Jawaban : C
Soal No.26 (UMB 2009)
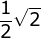

- 1


PEMBAHASAN :
Diketahui:
Panjang rusuk = 2cm
Titik tengah AE = P
Titik tengah BF = Q
Titik tengah BC = R
Titik tengah AD = S
Panjang BR = AS = ![]() cm
cm
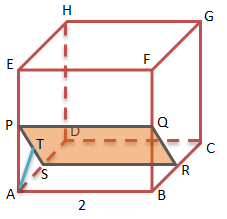
Menentukan jarak A ke bidang PQRS (AT)
Perbandingan luas segitiga pada daerah ΔPAS: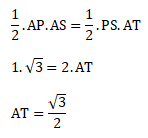
Jawaban : B
Soal No.27 (SIMAK UI 2011)
Diberikan kubus ABCD.RFGH dengan panjang rusuk 2cm. titik P terletak pada rusuk FG sehingga FP = 2PG. Jika α adalah bidang irisan kubus yang melalui titik B, D, dan P maka luas bidang α adalah … cm2 .
PEMBAHASAN :
Diketahui:
Panjang rusuk = 2cm
FP = 2PG
Bidang α = trapesium BDPQ
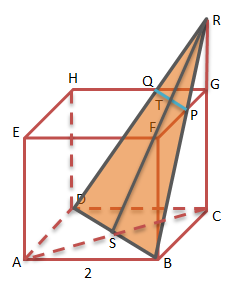
Penyelesaian 1:
Panjang FG = panjang rusuk
FG = 2
FP + PG = 2
2PG + PG = 2
3PG = 2![]()
Penyelesaian 2:
Perhatikan DBCR dan DPGR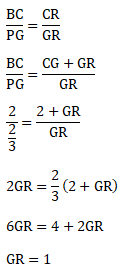
Maka CR = CG + GR = 2 + 1 = 3
Penyelesaian 3:
Perhatikan gambar DSCR di bawah ini: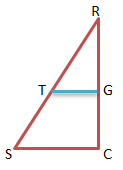
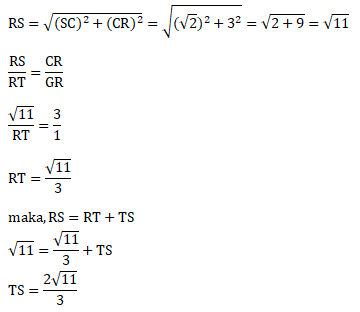
Penyelesaian 4:
Perhatikan DDBR: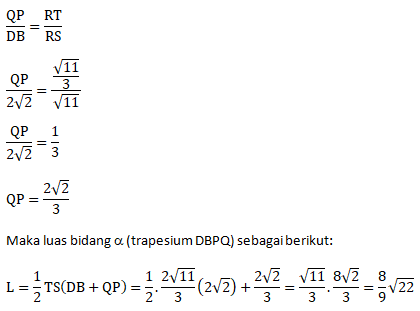
Jawaban : A
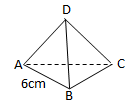
Soal No.27 (SIMAK UI 2012)
PEMBAHASAN :
Diketahui:
BC ⊥ BD
AB ⊥ bidang BCD
BC = BD = ![]()
AB = a cm
CE = ED = ½ CD = a
Perhatikan gambar segitiga berikut: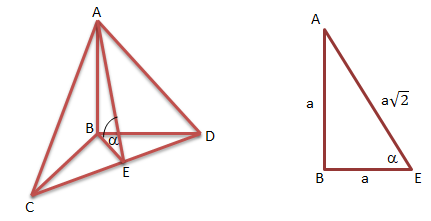
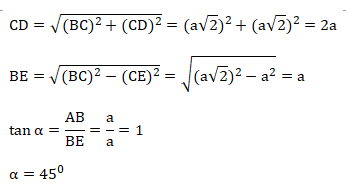
Jawaban : B
Soal No.28 (SNMPTN 2007)
PEMBAHASAN :
Diketahui:
∠EBA = ![]()
∠GBC = ![]()
Balok ABCD.EFGH: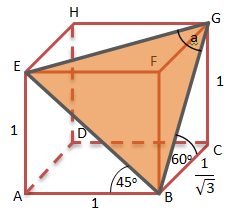
Menentukan BC
Untuk menentukan sin dengan menggunakan aturan cos, sebagai berikut:

Jawaban : A
Soal No.29 (SIMAK UI 2013)
Diberikan suatu limas segiempat beraturan T.ABCD dengan sisi tegak berupa segitiga sama sisi. Titik Q terletak pada sisi TA, di mana perbandingan TQ : QA = 1 : 2, sedangkan R terletak di sisi TC, dengan perbandingan TR : RC = 2 : 1. Jika titik S terletak di sisi TB, di mana RS sejajar CB, besar sudut TSQ adalah …
PEMBAHASAN :
Diketahui:
Titik Q terletak pada sisi TA
TQ : QA = 1 : 2
Titik R terletak di sisi TC
TR : RC = 2 : 1
Titik S terletak di sisi TB
Misalkan, panjang sisinya = 3 cm
Limas segiempat beraturan T.ABCD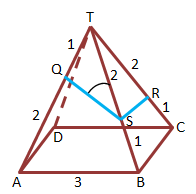
∠T = 600 (sisi tegak berupa segitiga sama sisi)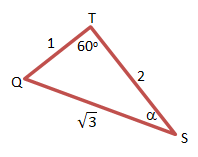
Perhatikan QTS, dengan sudut siku-siku di Q, dengan aturan cos panjang sisi QS adalah
Jawaban : E
Semoga Bermanfaat