Rangkuman Materi, Contoh Soal & Pembahasan Garis & Sudut SMP

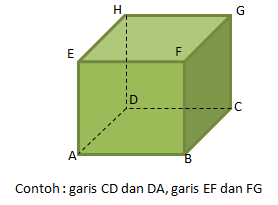
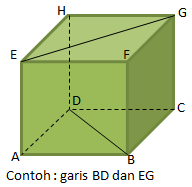
Garis

Kedudukan Dua Garis

Macam-macam kedudukan dua garis:

1. Dua garis sejajar, yaitu dua garis sejajar yang berada dalam satu bidang datar yang tidak akan pernah bertemu atau berpotongan walaupun kedua garis tersebut diperpanjang hingga tak berhingga. Garis sejajar dilambangkan dengan “ // “. Garis sejajar memiliki sifat-sifat sebagai berikut:
2. Melalui sebuah titik di luar garis dapat ditarik sebuah garis lurus lain yang sejajar.
3. ketika sebuah garis memotong salah satu dari dua garis yang sejajar maka garis tersebut akan memotong garis yang lain.
4. Apabila sebuah garis sejajar dengan dua garis lainnya maka kedua garis itu akan saling sejajar satu sama lain.
   
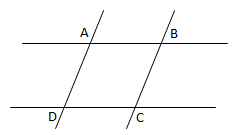
5. Dua garis berpotongan, yaitu dua buah garis yang terletak pada bidang datar dan berpotongan di satu titik potong (titik persekutuan).
   
6. Dua garis berimpit, yaitu dua garis terletak pada satu garis lurus sehingga setidaknya memiliki dua titik potong.
   
7. Dua garis bersilangan, yaitu dua garis yang tidak sejajar, tidak terletak pada satu bidang datar, dan tidak akan berpotongan jika diperpanjang.
   

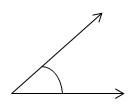
Sudut

Sudut merupakan suatu daerah yang terbentuk dari sebuah sinar yang diputar pada pangkal sinarnya  atau pertemuan dua ruas garis yang bertemu pada satu titik. Sudut dilambangkan dengan symbol “Д dan  satuannya adalah derajat (⁰ ).

Macam – Macam Sudut

Berdasarkan besar sudutnya, sudut dibedakan menjadi:

1. Sudut lancip: sudut yang besar sudutnya antara 0⁰ – 90⁰ .
   
2. Sudut tumpul: sudut yang besar sudutnya antara 90⁰ – 180.
   
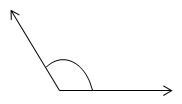
3. Sudut siku-siku: sudut yang besar sudutnya 90.
   
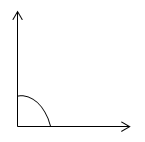
4. Sudut lurus: sudut yang besar sudutnya 180.
   
5. Sudut reflex: sudut yang besar sudutnya lebih dari 180⁰ tapi kurang dari 360.
   

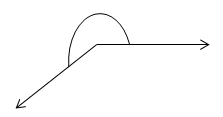
Hubungan Antarsudut

1. Sudut saling berpelurus (bersuplemen): besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180Contoh:
   
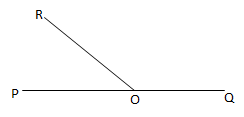
   ∠POR  + ∠QOR  = 180
   Contoh:
   ∠P = 60⁰ , maka suplemennya = 180⁰ –  60⁰  = 120
2. Sudut saling berpenyiku (berkomplemen): besar jumlah dua sudut yang berpenyiku adalah 90
   
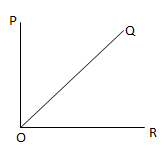
   ∠POQ + ∠QOR = 90
   Contoh:
   ∠P = 35 , maka komplemennya = 90 – 35 = 65
   1. Sudut saling bertolak belakang: dua sudut yang saling bertolak belakang memiliki besar sudut yang sama. Sudut tersebut letaknya saling membelakangi.
      Contoh: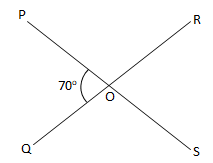
      
      ∠POQ = ∠ROS = 75

Hubungan Antarsudut Jika Dua Garis Sejajar Dipotong Oleh Sebuah Garis Lurus 

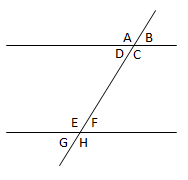
1. Sudut-sudut sehadapBesar sudutnya sama besar yaitu:
   ∠A = ∠E
   ∠B = ∠F
   ∠C = ∠H
   ∠D = ∠G
2. Sudut-sudut bersebrangan
   Besar sudutnya sama besar, dibagi menjadi dua yaitu:
   • Dalam bersebrangan
     ∠C = ∠E
     ∠D = ∠F
   • Luar bersebrangan
     ∠A = ∠G
     ∠B = ∠H
3. Sudut-sudut dalam sepihak
   Sudut-sudut sepihak membentuk sudut 180
   ∠D + ∠E = 180
   ∠C + ∠F = 180
4. Sudut-sudut luar sepihak
   Sudut-sudut luar sepihak membentuk sudut 180
   ∠B + ∠G = 180
   ∠A + ∠H = 180

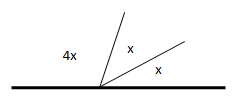
Soal No.1

Sudut yang terbesar adalah…

1. 60^o
2. 90^o
3. 120^o
4. 150^o

PEMBAHASAN :
Jumlah sudut adalah 180^o
Maka:
4x + x + x = 180^o
6x = 180^o
x = 30^o
Sudut yang terbesar adalah 4x sehingga sudutnya
4x = 4. 30^o = 120^o
Jawaban C

Soal No.2

Jika sudut yang saling berpenyiku memiliki perbandingan 10 : 8. Besar sudut yang terbesar adalah….

1. 40^o
2. 50^o
3. 90^o
4. 120^o

PEMBAHASAN :
Sudut yang saling berpenyiku memiliki jumlah sudut = 90^o


Maka sudut yang terbesarnya adalah 50^o
Jawaban B

Soal No.3

Jika diketahui ∠P = (2x + 8)^o dan ∠Q = (x – 5)^o. Kedua sudut tersebut berpenyiku maka ∠Q adalah….

1. 24^o
2. 60^o
3. 75^o
4. 82^o

PEMBAHASAN :
Jumlah sudut berpenyiku = 90^o
∠P + ∠Q = 90^o
(2x + 8) + (x – 5) = 90
2x + x + 8 – 5 = 90
3x + 3 = 90
3x = 90 – 3 = 87

maka ∠Q
∠Q = x – 5 = 29 – 5 = 24^o
Jawaban A

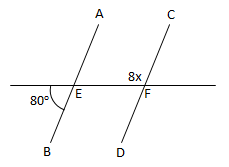
Soal No.4
Diketahui gambar sebagai berikut

Jika AB sejajar CD maka besar x adalah….

1. 1. 10^o
   2. 12,5^o
   3. 30^o
   4. 45^o
   5. 60^o

PEMBAHASAN :
Menentukan ∠FEB
∠FEB = 180^o – 80^o = 100^o
∠CFE akan sama dengan ∠FEB karena merupakan pasangan sudut luar bersebrangan
∠CFE = 100^o = 8x
8x = 100^o
x = 12,5^o
Jawaban C

Soal No.5

Dari pelurusnya besar sebuah sudut adalah 7 : 11. Maka besar sudut tersebut adalah…

1. 50^o
2. 60^o
3. 70^o
4. 80^o

PEMBAHASAN :
Diketahi perbandingan sudut dengan pelurusnya adalah 7 : 11. Jika dijumlahkan dua sudut yang saling berpelurus jumlahnya adalah 180^o
Menentukan besarnya sudut

Jawaban C

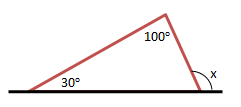
Soal No.6

Besar sudut x adalah

1. 120^o
2. 130^o
3. 150^o
4. 160^o

PEMBAHASAN :
Jumlah sudut dalam segitiga = 180^o
Sudut segitiga di dekat x adalah
180 – (100 + 30) = 50^o
Maka sudut x adalah
x + 50^o = 180^o
x = 180^o – 50^o = 130^o
Jawaban B

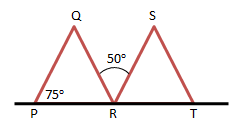
Soal No.7

besar ∠PRQ adalah….

1. 30^o
2. 40^o
3. 50^o
4. 60^o

PEMBAHASAN :
∠QPR sehadap dengan ∠SRT maka
∠SRT sama dengan ∠QPR yaitu 75^o
Jumlah sudut dalam segitiga adalah 180^o
maka ∠PRQ = 180 – (75 + 55) = 180 – 130 = 50^o
Jawaban C

Soal No.8

Besarnya x adalah….

PEMBAHASAN :
Jumlah sudutnya adalah 180^o
Maka:
4x + 90 + 3x + 6 = 180
7x + 96 = 180
7x = 180 – 96 = 84
7x = 84
x = 12
Jawaban A

Soal No.9

Jika diketahui titik P, Q, dan R terletak segaris dengan perbandingan PQ : QR = 8 : 13. Panjang PQ = 42 cm. Maka panjang garis PR adalah….cm

PEMBAHASAN 
Menentukan panjang QR melalui perbandingan

Maka panjang PR
PR = PQ + QR = 42 + 26 = 68 cm
Jawaban B

Soal No.10

Diketahui selisih ∠BAD dan ∠ ADC adalah 40^o maka besar ∠ADC adalah

1. 60^o
2. 70^o
3. 80^o
4. 85^o

PEMBAHASAN :
∠BAD dijumlahkan ∠ADC akan menghasilkan sudut 180^o
∠BAD + ∠ADC = 180^o
Jika ∠ADC = a, maka ∠BAD
∠BAD – ∠ADC = 40^o
∠BAD – a = 40^o
∠BAD = 45^o + a
Sehingga
∠BAD + ∠ADC = 180
(40 + a) + a = 180
40 + 2a = 180
2a = 180 – 40 = 140
2a = 140
a = 70^o = ∠ADC
Jawaban B

Perhatikan gambar di bawah ini!
Gambar untuk soal nomor 11 – 14.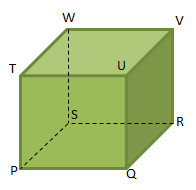

Soal No.11

Garis sejajar pada gambar di atas adalah …

1. PT dan PQ
2. PR dan UW
3. PQ dan SR
4. TU dan VW

PEMBAHASAN :

• PT dan PQ = berpotongan
• PR dan UW = bersilangan
• PQ dan SR = sejajar
• TU dan UV = berpotongan

Jawaban C

Soal No.12

Garis – garis horizontal pada gambar di atas adalah sebagai berikut, kecuali  …

1. SW
2. PQ
3. RS
4. VW

PEMBAHASAN :

• SW = vertical
• PQ = horizontal
• RS = horizontal
• VW = horizontal

Jawaban A

Soal No.13

Yang termasuk garis bersilangan pada gambar di atas adalah …

1. PT dan PQ
2. PR dan UW
3. PQ dan SR
4. TU dan VW

PEMBAHASAN :

• PT dan PQ = berpotongan
• PR dan UW = bersilangan
• PQ dan SR = sejajar
• TU dan UV = berpotongan

Jawaban B

Soal No.14

Yang termasuk garis berpotongan pada gambar di atas adalah …

1. PT dan UW
2. PR dan UW
3. PQ dan SR
4. TU dan VW

PEMBAHASAN :

• PT dan UW = bersilangan
• PR dan UW = bersilangan
• PQ dan SR = sejajar
• TU dan UV = berpotongan

Jawaban D

Soal No.15

Yang termasuk contoh sudut tumpul adalah …

PEMBAHASAN :

• 
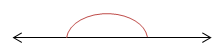
  Sudut lurus: besar sudutnya 180
• 
  Sudut tumpul: besar sudutnya  antara 90⁰ – 180
• 
  Sudut lancip: besar sudutnya antara 0⁰ – 90
• 
  Sudut siku-siku: besar sudutnya 90

Jawaban B

Soal No.16

Pada sebuah segitiga tumpul memiliki sudut lancip sebanyak … buah.

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Di bawah ini adalah gambar segitiga tumpul: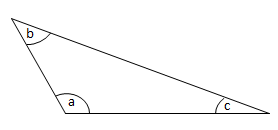

∠a = sudut tumpul
∠b = sudut lancip
∠c = sudut lancip
Maka sudut lancip pada segitiga tumpul ada 2 buah
Jawaban B

Soal No.17

Pada segitiga sama kaki jenis sudutnya adalah …

1. Siku – siku
2. Lurus
3. Lancip
4. Tumpul

PEMBAHASAN :
Perhatikan gambar segitiga sama kaki di bawah ini!

ketiga sudut pada segitiga sama kaki di atas adalah sudut lancip.
Jawaban C

Soal No.18

Perhatikan gambar di bawah ini!

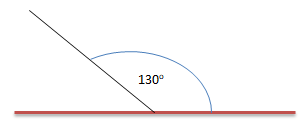
Pelurus sudut pada gambar di atas adalah …

1. 50
2. 60
3. 70
4. 80

PEMBAHASAN :
Sudut saling berpelurus (bersuplemen): besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180⁰ . Maka besar sudut pada gambar di atas dapat dihitung sebagai berikut:
180⁰ – 130⁰ = 50⁰
Jawaban A

Soal No.19

Perhatikan gambar di bawah ini!

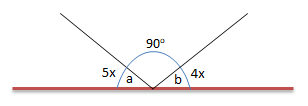
Besar sudut a dan b pada gambar di atas adalah …

1. 30⁰ dan 40⁰
2. 60⁰ dan 30⁰
3. 40⁰ dan 50
4. 50⁰ dan 40

PEMBAHASAN :
Pada gambar di atas berlaku sudut saling berpelurus atau bersuplemen yang besarnya adalah 180⁰ .
⇔ 5x + 90⁰ + 4x = 180
⇔ 9x + 90⁰ = 180⁰
⇔ 9x = 90
⇔ x = 10⁰

Maka sudut a dan b dapat dihitung sebagai berikut:
∠a = 5x = 5 . 10⁰ = 50⁰
∠b = 4x = 4 . 10⁰ = 40⁰
Jawaban D

Soal No.20

Perhatikan gambar di bawah ini!

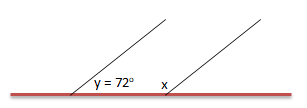
Besar sudut x adalah …

1. 90
2. 108
3. 120
4. 150

PEMBAHASAN :
Pada gambar di atas sudut x dan y adalah sudut dalam sepihak. Sudut dalam sepihak membentuk sudut 180⁰ . Maka sudut x dapat dihitung sebagai berikut:
x + y = 180
x = 180 – y
⇔ 180⁰ – 72⁰ = 108⁰
Jawaban B

Soal No.21

Perhatikan gambar di bawah ini!

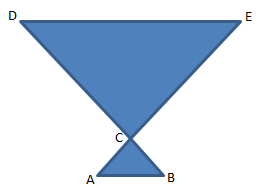
Sudut bertolak belakang yang sesuai dengan gambar di atas adalah …

1. ∠ABC = ∠CDE
2. ∠DCE = ∠ACB
3. ∠CAB = ∠CED
4. ∠ACD ≠ ∠ACB

PEMBAHASAN :

• ∠ABC = ∠CDE (sudut dalam bersebrangan)
• ∠DCE = ∠ACB (sudut bertolak belakang)
• ∠CAB = ∠CED (sudut dalam bersebrangan)
• ∠ACD ≠ ∠ACB (sudut saling berpelurus)

Jawaban B

Soal No.22

Perhatikan gambar di bawah ini!

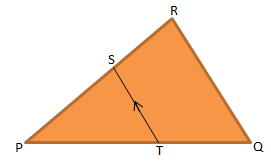
Besar ∠SPT adalah …

1. 25
2. 50
3. 75
4. 100

PEMBAHASAN :
Diketahui:
Garis ST//QR = sejajar
∠PST = ∠PRQ = 80⁰ = sehadap

Jumlah sudut segitiga = 180⁰
∠SPT + ∠PST + ∠PTS = 180⁰
∠SPT + 80⁰ + 75⁰ = 180⁰
∠SPT = 180⁰ – (80⁰ + 75⁰ )
∠SPT = 25
Jawaban A

Soal No.23

Perhatikan gambar di bawah ini!

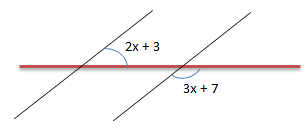
Besar nilai x pada gambar tersebut = … ⁰

1. 31
2. 34
3. 37
4. 42

PEMBAHASAN :
Jumlah sudut pada gambar tersebut = 180⁰
Maka nilai x dapat dihitung sebagai berikut:
(2x + 3) + (3x + 7) = 180⁰
5x + 10 = 180⁰
5x = 170⁰
x = 34
Jawaban B

Soal No.24

Perhatikan gambar di bawah ini!

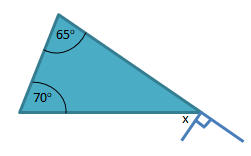
Besar nilai x pada gambar tersebut = … ⁰

1. 15
2. 25
3. 35
4. 45

PEMBAHASAN :
Jumlah besar sudut pada segitiga = 180⁰
Maka untuk menghitung nilai x adalah:
70⁰ + 65⁰ + (90⁰ – x) = 180⁰  
225⁰ – x = 180⁰
x = 45
Jawaban D

Soal No.25

Perhatikan gambar di bawah ini!

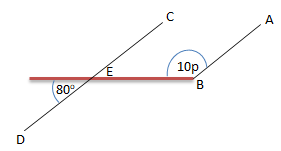
Garis CD//AB, maka besar nilai p adalah …

1. 5
2. 10
3. 15
4. 20

PEMBAHASAN :
Diketahui:
Garis CD//AB
∠BED saling berpelurus = 180⁰ – 80⁰ = 100
∠ABE = ∠BED = pasangan sudut luar bersebrangan

Maka besar nilai p dapat dihitung sebagai berikut:
⇔ 100⁰ = 10p
⇔ p = 10
Jawaban D

Di bawah ini adalah gambar untuk no. 26 – 30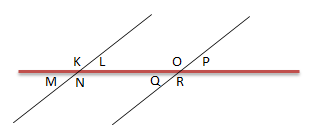

Diketahui ∠K = 120

Soal No.26

Besar ∠M adalah …

1. 60
2. 80
3. 120
4. 180

PEMBAHASAN :
∠K dan ∠M adalah pasangan sudut berpelurus, besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180
Maka nilai M = 180⁰ – 120⁰ = 60
Jawaban A

Soal No.27

Besar ∠O adalah …

1. 100
2. 110
3. 120
4. 180

PEMBAHASAN :
∠K dan ∠O adalah pasangan sehadap, besar sudut-sudutnya sama besar.
∠K = ∠O = 120
Jawaban C

Soal No.28

Besar ∠R adalah …

1. 180
2. 120
3. 60
4. 30

PEMBAHASAN :
∠R bertolak belakang dengan ∠O, besar sudut-sudutnya sama besar.
∠R = ∠O = 120
Jawaban B

Soal No.29

∠M dan ∠P hubungan antarsudutnya adalah …

1. Dalam bersebrangan
2. Luar bersebrangan
3. Sehadap
4. Bertolak belakang

PEMBAHASAN :
∠M dan ∠P merupakan pasangan sudut luar bersebrangan  dengan besar sudut sama besar.
Jawaban B

Soal No.30

∠L dan ∠O hubungan antarsudutnya adalah …

1. Dalam bersebrangan
2. Luar bersebrangan
3. Dalam sepihak
4. Luar sepihak

PEMBAHASAN :
∠L dan ∠O merupakan pasangan sudut dalam sepihak, Sudut-sudut dalam sepihak membentuk sudut 180.
Jawaban C

Soal No.31

Besar ∠Q adalah …

1. 60
2. 120
3. 180
4. 30

PEMBAHASAN :
∠Q berpelurus dengan ∠O, besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180

Maka, besar ∠Q = 180⁰ – ∠O
⇔ 180⁰ – 120
⇔ 60
Jawaban A

Soal No.32

Perhatikan gambar berikut ini!

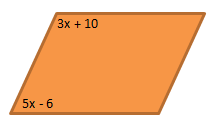
Besar sudut tumpulnya adalah …

1. 101
2. 102
3. 103
4. 104

PEMBAHASAN :
Diketahui:
Bahwa jumlah sudut pasangan sudut lancip dan sudut tumpul pada jajargenjang adalah 180
Sudut tumpul = 5x –  6
Sudut lancip = 3x + 10

Menentukan nilai x:
(3x + 10) + (5x – 6) = 180
8x + 4 = 180⁰
8x = 176⁰
x = 22⁰

Maka besar sudut tumpulnya dapat dihitung sebagai berikut:
Besar sudut tumpul = 5x –  6
⇔ 5 (22) – 6
⇔ 104
Jawaban D

Soal No.33

Diketahui titik P, Q, dan R terletak pada satu garis dengan perbandingan PQ : QR adalah 5 : 3 cm. sedangkan panjang garis PQ adalah 30 cm, maka panjang garis PR adalah … cm.

1. 42
2. 48
3. 50
4. 62

PEMBAHASAN :
Diketahui:
PQ : QR = 5 : 3 cm
Panjang garis PQ = 30 cm

Menentukan panjang garis QR sebagai berikut: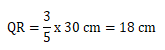

Maka panjang garis PR = PQ + QR
⇔ 30 cm + 18 cm
⇔ 48 cm
Jawaban B

Soal No.34

Perhatikan gambar berikut!

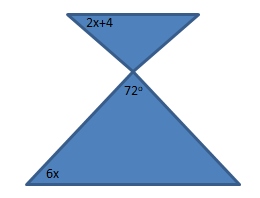
Besar nilai x = … ⁰

1. 12
2. 13
3. 14
4. 15

PEMBAHASAN :
Pada gambar di atas terdapat sudut yang bertolak belakang dan sudut yang bersebrangan. Sudut-sudut tersebut memiliki besar sudut yang sama. Sehingga diperoleh gambar sebagai berikut: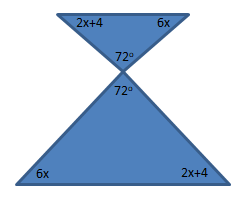

Jumlah besar sudut pada segitiga = 180⁰

Maka besar nilai dapat dihitung sebagai berikut:
(2x + 4) + 6x + 72⁰ = 180
8x + 76⁰ = 180
8x = 104⁰
x = 13
Jawaban B

Soal No.35

Perhatikan gambar berikut!

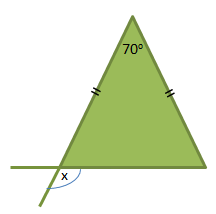
Besar nilai x = …

1. 125
2. 130
3. 145
4. 180

PEMBAHASAN :
Gambar di atas merupakan segitiga sama kaki, dengan dua sudut yang sama besar yang diapit oleh alas dan kakinya. Jumlah besar sudut segitiga adalah 180⁰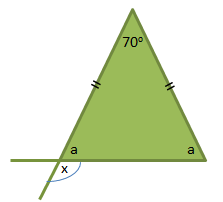

70⁰ + 2a = 180⁰
2a = 110⁰
a = 55
∠a dan ∠x berpelurus, besar sudut saling berpelurus adalah 180
∠x = 180⁰ – 55⁰
∠x = 125
Jawaban A

Soal No.36

Perhatikan gambar berikut!

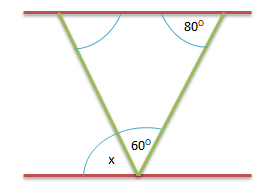
Besar nilai x = …

1. 60
2. 180
3. 40
4. 70

PEMBAHASAN :
Jumlah sudut segitiga = 180
180⁰ – (80⁰ + 60⁰ ) = 40⁰  (pasangan sudut dalam bersebrangan dari ∠x)
Pada gambar tersebut terdapat pasangan sudut dalam bersebrangan (besar sudut sama), sehingga ∠x = 40
Jawaban C

Soal No.37

Perhatikan gambar di bawah ini!

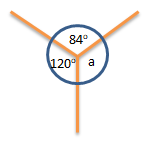
besar sudut a = … ⁰

1. 144
2. 156
3. 162
4. 122

PEMBAHASAN :
Jumlah sudut pada gambar di atas adalah 360⁰
Maka ∠a = 360⁰ – (84⁰ + 120⁰ )
⇔ 360⁰ – 204
⇔ 156
Jawaban C

Soal No.38

Selisih dua buah sudut berpenyiku adalah 36⁰ . Sudut dengan nilai terbesar adalah … ⁰

1. 45
2. 63
3. 56
4. 67

PEMBAHASAN :
Diketahui:
Sudut berpenyiku berjumlah = 90⁰
Selisih sudut = 36
Misalkan sudut saling berpenyiku x dan x + 36⁰
⇔ x + (x + 36⁰ ) = 90
⇔ 2x = 54
⇔ x = 27

Maka sudut dengan nilai terbesar = x + 36⁰
⇔ 27⁰ + 36⁰
⇔ 63⁰
Jawaban B

Soal No.39

Perhatikan gambar di bawah ini!

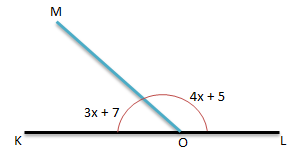
Besar ∠MOL adalah …

1. 123
2. 164
3. 141
4. 101

PEMBAHASAN :
(3x + 7) + (4x + 5) (pasangan sudut berpelurus)
Jumlah sudut berpelurus = 180

Menentukan nilai x, sebagai berikut:
(3x + 7) + (4x + 5) = 180⁰
7x + 12 = 180⁰
7x = 168
x = 24

Maka, ∠MOL = 4x + 5
⇔ 4 (24) + 5
⇔ 101
Jawaban D

Soal No.40

Berikut adalah pasangan sudut yang memiliki besar sudut sama adalah …

1. Pasangan sudut berkomplemen
2. Pasangan sudut bersuplemen
3. Pasangan sudut bertolak belakang
4. Pasangan sudut dalam sepihak

PEMBAHASAN :

• Pasangan sudut berkomplemen/ berpenyiku: besar jumlah dua sudut yang berpenyiku adalah 90⁰
• Pasangan sudut bersuplemen: besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180⁰ .
• Pasangan sudut bertolak belakang: dua sudut yang saling bertolak belakang memiliki besar sudut yang sama. Sudut tersebut letaknya saling membelakangi.
• Pasangan sudut dalam sepihak: Sudut-sudut dalam sepihak membentuk sudut 180.

Maka, pasangan sudut yang memiliki besar sudut sama adalah pasangan sudut bertolak belakang.
Jawaban C