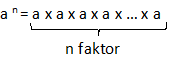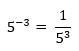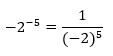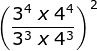Untuk Pembelajaran selanjutnya…
Bilangan berpangkat bilangan bulat
Bilangan berpangkat merupakan perkalian berulang dari suatu bilangan yang sama.
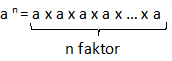
a = bilangan pokok
n = pangkat/eksponen
contoh:
34 = 3 x 3 x 3 x 3 = 81
Bilangan pangkat nol
Semua bilangan apabila a ≠ 0 jika dipangkatkan 0 hasilnya sama dengan 1
a 0 = 1
contoh:
Bilangan pangkat bulat positif
Pada bilangan pangkat bulat positif berlaku sifat-sifat:
-
a p x a q = a p+q
contoh:
23 x 25 = 23+5 = 28
-

Contoh:

-
(ap )q = apxq = aqxp
Contoh:
(-34 )2 = (-3)4×2 = -38
-
ap + aq = ap (1 + aq-p ), q ≥ p
contoh:
53 + 57 = 53 (1+57-3 ) = 53 (1+54 )
-
ap – aq = ap (1- aq-p ), q ≥ p
contoh:
64 – 69 = 64 (1-69-4 ) = 64 (1-65 )
Bilangan pangkat bulat negatif
Pada bilangan pangkat bulat negatif berlaku sifat:
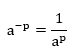 , a ≠ p
, a ≠ p
Contoh:
Bilangan rasional berpangkat bulat
Bilangan rasional berpangkat bulat perlakuannya sama seperti pada bilangan berpangkat bilangan bulat.
Contoh:
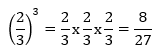
Bentuk Akar
Bentuk akar merupakan bilangan irasional. Bilangan irasional adalah bilangan real yang tidak bisa dibagi. Contoh bilangan bentuk akar adalah:
 adalah bentuk akar, karena bilangannya irasional
adalah bentuk akar, karena bilangannya irasional adalah bentuk akar, karena bilangannya irasional
adalah bentuk akar, karena bilangannya irasional
Sedangkan:
 bukan bentuk akar, karena
bukan bentuk akar, karena  = 3 yang merupakan bilangan rasional
= 3 yang merupakan bilangan rasional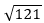 bukan bentuk akar, karena
bukan bentuk akar, karena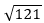 = 11 yang merupakan bilangan rasional
= 11 yang merupakan bilangan rasional
Menyederhanakan bentuk akar
-
 , a dan b adalah bilangan real positif
, a dan b adalah bilangan real positifContoh:
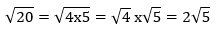
-
 , a dan b > 0
, a dan b > 0Contoh:

Operasi aljabar untuk bentuk akar
Sifat-sifat yang berlaku adalah:
-
 , berlaku juga untuk pengurangan
, berlaku juga untuk penguranganContoh:
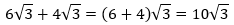
-
 , a dan b ≥ 0
, a dan b ≥ 0Contoh:
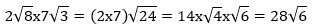
-
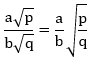 , a dan b ≥ 0
, a dan b ≥ 0Contoh:
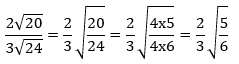
Merasionalkan penyebut suatu pecahan
Cara merasionalkannya adalah:
Bilangan berpangkat pecahan
Bilangan berpangkat pecahan penyelesaiannya sebagai berikut:
![]() , a ≥ 0 dan p, q bilangan bulat positif
, a ≥ 0 dan p, q bilangan bulat positif
Contoh:
Soal No.1
- 120
- 133
- 144
- 150
PEMBAHASAN :
Ingat ![]()
Maka: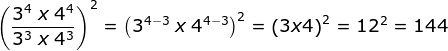
Jawaban C
Soal No.2
Jika diketahui 1,542 = 2,3716, maka 1542 adalah….
- 237.160
- 23.716
- 237,16
- 23,716
PEMBAHASAN :
Jika di ubah bentuk 1,54 menjadi 154 x 100, maka
1542 = (1,54 x 100)2 = 1,542 x 1002 = 2,3716 x 10.000 = 23.716
Jawaban yang tepat adalah B
Jawaban B
Soal No.3
Bentuk sederhana dari 44 + 44 + 44 + 44 adalah….
…
PEMBAHASAN :
Bentuk sederhana dari 44 + 44 + 44 + 44 adalah 4 x 44
Jawaban C
Soal No.4
Nilai dari (4-1 + 3-2 + 7-1)-1 adalah….
PEMBAHASAN :
Ingat:![]()
maka :![]()
![]()
Jawaban C
Soal No.5
Jika diketahui 2a3 + 3a3 + a3 + 4a3 = 1.250maka nilai a2 + a adalah…
PEMBAHASAN :
2a3 + 3a3 + a3 + 4a3 = (2+3+1+4) a3 = 10a3 = 1.250
a3 = 1.250/10 = 125![]()
maka nilai a2 + a = 52 + 5 = 25 + 5 = 30
Jawaban C
Soal No.6
Soal No.7
Jawaban A
Soal No.8
Soal No.9
Hasil dari 2a3b2c2 x 4a-2bc-3…
- 4ab3c-1
- 8ab3c-1
- 8ab3c-2
- 4ab3c-2
Soal No.10
- 1,5
- 2
- 2,5
- 3
Soal No.11
Diketahui panjang sisi sebuah persegi 25 cm. maka luas persegi tersebut adalah … cm2
- 100
- 625
- 25
- 225
PEMBAHASAN :
Panjang sisi = s = 25 cm
Luas persegi dapat dihitung dengan rumus sebagai berikut:
L = s x s
L = 25 cm x 25 cm
L = 625 cm2
Jawaban B
Soal No.12
Persamaan garis (2x + 1)2 = 225, x > 0, maka nilai x adalah …
PEMBAHASAN :
Akar kuadrat dari 225 = 152
Maka nilai x dapat dihitung sebagai berikut:
(2x + 1)2 = 225
(2x + 1)2 = 152
2x + 1 = 15
2x = 14
x = 7
Jawaban D
Soal No.13
Bentuk sederhana dari:

PEMBAHASAN :
Jawaban B
Soal No.14
Hasil perhitungan dari:

PEMBAHASAN :
Jawaban B
Soal No.15
Jika √5 = p maka √180 = …
PEMBAHASAN :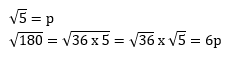
Jawaban A
Soal No.16
Hasil perhitungan dari
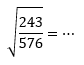
PEMBAHASAN :
Jawaban C
Soal No.17
Hasil perhitungan dari

PEMBAHASAN :
Jawaban B
Soal No.18
Hasil perhitungan dari 2√48 + 2√12 – √192 = …
PEMBAHASAN :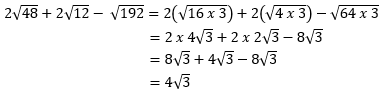
Jawaban D
Soal No.19
PEMBAHASAN :![]()
Jawaban A
Soal No.20
Bentuk sederhana dari √50 + √32 – √98 = …
- 5√2
- 4√2
- 3√2
- 2√2
PEMBAHASAN :
Jawaban D
Soal No.21
- 3

- 9
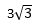
PEMBAHASAN :
Jawaban D
Soal No.22

PEMBAHASAN :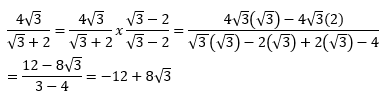
Jawaban A
Soal No.23

PEMBAHASAN :
Jawaban C
Soal No.24

PEMBAHASAN :
Jawaban A
Soal No.25
PEMBAHASAN :
Jawaban B
Soal No.26
- 35
- 45
- 55
- 65
PEMBAHASAN :
Maka x2 + 1 dapat dihitung sebagai berikut:
x2 + 1
⇒ 82 + 1
⇒ 65
Jawaban D
Soal No.27
PEMBAHASAN :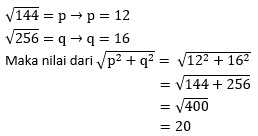
Jawaban B
Soal No.28
PEMBAHASAN :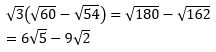
Jawaban A
Soal No.29
 …
…PEMBAHASAN :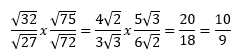
Jawaban D
Soal No.30
Pengurangan (45 )3 – (44 )3 = …
- 43 (45 – 44 )
- (45 – 44 )
- (48 – 47 )
- 42 (45 – 44 )
PEMBAHASAN :
(45 )3 – (44 )3 = 415 – 412 = 43 (45 – 44 )
Jawaban A
Soal No.31
PEMBAHASAN :![]()
Jawaban C
Soal No.32
PEMBAHASAN :![]()
Jawaban C
Soal No.33
PEMBAHASAN :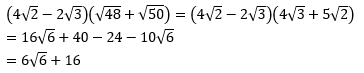
Jawaban A
Soal No.34
PEMBAHASAN :
Jawaban D
Soal No.35
PEMBAHASAN :
Jawaban C
Soal No.36
Diketahui sebuah bangun persegi memiliki panjang diagonal 36 cm. Maka luas persegi adalah …
- 256 cm2
- 648 cm2
- 560 cm2
- 480 cm2
PEMBAHASAN :
Jawaban B
Soal No.37
PEMBAHASAN :
Jawaban D
Soal No.38
PEMBAHASAN :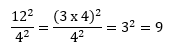
Jawaban C
Soal No.39
- 2x + 4y
- 3x – 4y
- 2x + 5y
- -4x – 3y
PEMBAHASAN :
Jawaban A
Soal No.40
- 4
- 6
- 8
- 10
PEMBAHASAN :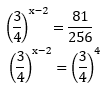
Maka nilai x:
x – 2 = 4
x = 6
Jawaban B
Semoga Bermanfaat