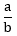Rangkuman Materi, Contoh Soal & Pembahasan Pecahan SD

Pengertian Pecahan

Pecahan dapat diartikan sebagai berikut:

• Bilangan yang mewakili suatu bagian dari keseluruhan
• Penulisan bilangan yang menyatakan bukan bilangan yang utuh
• Bentuk umum pecahan adalah 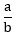, dengan a adalah pembilang dan b adalah penyebut (a dan b merupakan bilangan bulat dan  b ≠ 0).

Jenis –Jenis Pecahan

1. Pecahan Biasa
   Pecahan biasa adalah bentuk pecahan yang paling dasar dengan bentuk umum , sebagai perbandingan antara satu untuk semua atau sebagian dari suatu unit dengan nilai pembilang lebih kecil dibandingkan dengan penyebut. Contoh:
2. Pecahan Campuran
   Pecahan campuran adalah pecahan yang terdiri dari bilangan bulat dan pecahan biasa dengan pembilang lebih besar dibandingkan penyebutnya. Bentuk umum pecahan campuran  dengan a, b, dan c adalah anggota bilangan bulat. Contoh: .
3. Pecahan Desimal
   Pecahan desimal adalah pecahan yang dalam penulisannya menggunakan koma. Contoh 0,4   1,35   3,25
4. Pecahan Persen
   Pecahan persen adalah pecahan yang penyebutnya bernilai 100, dengan lambang % yang artinya per seratus. Contoh 20% , 57% , 62%
5. Pecahan Permil
   Pecahan permil adalah pecahan yang penyebutnya bernilai seribu, dengan lambang ‰ artinya per seribu. Contoh: 15‰, 42‰, 120‰

Menyederhanakan Pecahan

Pecahan-pecahan yang dapat disederhanakan adalah pecahan yang pembilang dan penyebutnya dapat dibagi dengan faktor persekekutuan.

Menyederhanakan pecahan dapat dilakukan dengan cara:

1. Menentukan faktor persekutuan terbesar (FPB) untuk pembilang dan penyebut
2. Membagi pembilang dan penyebut dengan FPB

Contoh:

Menentukan bentuk sederhana dari  adalah …

Tentukan FPB dari pembilang dan penyebut nya, sebagai berikut:

FPB dari 16 = 1,2,4,8,16

FPB dari 24 = 1,3,4,6,8,12,24

Maka FPB dari 16 dan 24 = 8

Bentuk sederhana dari

Mengubah Bentuk Pecahan

1. Mengubah bentuk pecahan biasa menjadi persen dan persen menjadi pecahan
   • Mengubah bentuk pecahan menjadi persen dengan cara membuat penyebut  menjadi 100, contohnya:
   • Mengubah bentuk pecahan biasa menjadi persen dengan cara mengalikan dengan 100% , contohnya:
   • Mengubah bentuk persen menjadi pecahan biasa dengan cara menjadikan penyebut bernilai  100 kemudian sederhanakan. Contohnya:
2. Mengubah bentuk pecahan menjadi desimal dan desimal menjadi pecahan biasa
   • Mengubah bentuk pecahan biasa menjadi desimal dengan cara membagi pembilang dengan penyebut, contohnya:
   • Mengubah bentuk pecahan biasa menjadi desimal dengan cara mengalikan penyebut sehingga  menjadi kelipatan 10, kemudian ubah ke bentuk desimal, contohnya:
   • Mengubah bentuk desimal menjadi pecahan biasa dengan cara menyatakan bentuk desimal kebentuk pecahan berpenyebut  kelipatan 10, kemudian sederhanakan. Contohnya:
3. Mengubah bentuk desimal menjadi persenMengubah bentuk desimal menjadi persen dengan cara mengalikan bentuk desimal dengan 100%, contohnya:0,2 x 100% = 20%
   • Mengubah bentuk desimal menjadi persen dengan cara menyatakan bentuk desimal ke pecahan biasa, kemudian kalikan dengan 100%, contohnya:
   • Mengubah bentuk desimal menjadi persen dengan cara menyatakan bentuk desimal ke pecahan berpenyebut 100 kemudian ubah dalam bentuk persen, contohnya:

Menentukan Nilai Pecahan

Nilai pecahan dari suatu bilangan dapat ditentukan dengan cara mengalikan pecahan dengan bilangan tertentu.

Contoh:
¼ dari 60 =⋯
¼ x 60 =   = 15
maka, ¼ dari 60 = 15

25% dari 500 ml adalah…
25% dari 500 ml = x 500 ml
=25 x 5 ml
=125 ml
maka,25% dari 500 ml adalah 125 ml

0,5 dari 100 kg adalah…
0,5 x 100 kg =  x 100 kg
= 5 x 10 kg
= 50 kg
maka,0,5 dari 100 kg adalah 50 kg

Operasi Hitung Pecahan

1. Penjumlahan
   Dua atau beberapa pecahan dapat dijumlahkan apabila penyebutnya bernilai sama. Apabila penyebut pada pecahan tersebut nilainya berbeda maka samakan terlebih dahulu dengan mencari nilai KPK nya. Rumus yang berlaku pada operasi hitung penjumlahan pecahan yaitu:
   
   Contoh:
   
   Untuk menjumlahkan pecahan desimal, jumlahkan tiap angka sesuai nilai tempatnya yaitu puluhan lurus dengan puluhan, satuan lurus dengan satuan, koma lurus dengan koma, persepuluh lurus dengan persepuluh, dan perseratus lurus dengan perseratus.
   Contoh:
   10,25 + 26,12 = …
   10,25
   26,12    +
   36,37
2. Pengurangan
   Dua atau beberapa pecahan dapat dikurangkan apabila penyebutnya bernilai sama. Apabila penyebut pada pecahan tersebut nilainya berbeda maka samakan terlebih dahulu dengan mencari nilai KPK nya. Rumus yang berlaku pada operasi hitung pengurangan pecahan yaitu:
   
   Contoh:
   
   Untuk mengurangkan pecahan desimal, kurangkan tiap angka sesuai nilai tempatnya yaitu puluhan lurus dengan puluhan, satuan lurus dengan satuan, koma lurus dengan koma, persepuluh lurus dengan persepuluh, dan perseratus lurus dengan perseratus.
   Contoh:
   19,68 – 12,32 = …
   19,68
   12,32      –
   7,36
3. Perkalian
   Perkalian pada dua bentuk pecahan atau beberapa pecahan dapat diselesaikan dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Rumus yang berlaku pada operasi hitung perkalian pecahan yaitu:
   
   Contoh:
   
   Sedangkan perkalian untuk bentuk pecahan desimal dapat diselesaikan dengan cara-cara sebagai berikut:
   • Menghitung banyak angka di belakang koma pada masing-masing bilangan kemudian jumlahkan.
   • mengalikan setiap bilangan desimal seperti perkalian pada bilangan bulat.
   • meletakkan tanda koma pada bilangan hasil operasi hitung sesuai dengan jumlah angka di belakang koma yang sudah dijumlahkan.

   Contoh:
   1,56 x 3,136 = …
   Jumlah angka di belakang koma pada bilangan pertama 2 angka di belakang koma dan bilangan kedua 3 angka di belakang koma. Maka jumlah angka di belakang koma pada kedua bilangan adalah 5 angka di belakang koma.
   156 x 3136 = 489216
   1,56 x 3,136 = 4,89216

4. Pembagian
   Pembagian pada bentuk pecahan dapat diselesaikan dengan mengalikan pecahan pertama  dengan pecahan kedua yang sudah dibalik posisinya (pertukaran pembilang menjadi penyebut dan penyebut menjadi pembilang). Rumus yang berlaku pada operasi hitung pengurangan pecahan yaitu:
   
   Contoh:
   
   Sedangkan untuk pembagian bentuk pecahan desimal dapat diselesaikan  dengan cara sebagai berikut:
   • Mengubah pecahan desimal menjadi pecahan biasa.
   • Pembagian dilakukan seperti yang berlaku pada operasi hitung pembagian bentuk pecahan biasa
5. Operasi Hitung CampuranBeberapa syarat yang berlaku untuk operasi hitung campuran yaitu:
   • Untuk operasi hitung dengan (+) dan (-) maka bilangan dihitung dari sebelah kiri
   • Untuk operasi hitung dengan (x) dan (:) maka bilangan dihitung dari sebelah kiri
   • Untuk operasi hitung (+), (-), (x), dan (:) maka bilangan dihitung dari operasi hitung (x) atau (:) kemudian operasi hitung (+) atau (-)
   • Untuk operasi hitung yang memakai tanda kurung maka bilangan di dalam tanda kurung dikerjakan terlebih dahulu

Soal No.1

Bentuk sederhana dari pecahan adalah …

PEMBAHASAN :
Untuk menentukan pecahan sederhana dari bentuk pecahan di atas adalah dengan mencari FPB dari pembilang dan penyebut.

FPB dari 48 = 2 x 2 x 2 x 2 x 3 = 2⁴  x 3
FPB dari 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
FPB dari 48 dan 72 adalah 2³ x 3 = 24

Maka bentuk sederhana dari pecahan di atas adalah:

Jawaban B

Soal No.2

Bentuk persen dan desimal dari pecahan biasa adalah …

1. 30% dan 0,3
2. 35% dan 0,35
3. 25% dan 0,25
4. 40% dan 0,4

PEMBAHASAN :
Mengubah bentuk pecahan biasa menjadi persen bisa dengan cara mengalikan dengan 100%

Mengubah bentuk pecahan biasa menjadi desimal dengan cara mengalikan penyebut sehingga  menjadi kelipatan 10, 100, 1.000 dst kemudian ubah ke bentuk desimal.

Jawaban A

Soal No.3

Bentuk pecahan campuran sederhana dari bilangan persen 136% adalah …

PEMBAHASAN :
Mengubah bentuk persen menjadi pecahan biasa dengan cara menjadikan penyebut bernilai  100 kemudian sederhanakan.

Jawaban D

Soal No.4

Tentukan nilai pecahan dari 120 adalah …

1. 30
2. 40
3. 48
4. 52

PEMBAHASAN :
Nilai pecahan dari suatu bilangan dapat ditentukan dengan cara mengalikan pecahan dengan bilangan tertentu.

Jawaban C

Soal No.5

Berikut beberapa bentuk pecahan, yaitu 25%; ; 0,8 ; urutan pecahan dari nilai terkecil  adalah …

PEMBAHASAN :
Pada soal di atas bentuk pecahan belum sejenis. Untuk mengurutkan pecahan tersebut, ubah pecahan terlebih dahulu ke bentuk pecahan misalnya kebentuk desimal.

Maka urutan dari yang terkecil yaitu:
Jawaban A

Soal No.6

Hasil perhitungan dari adalah …

1. 4
2. ½
3. 3
4. 2

PEMBAHASAN :

Jawaban D

Soal No.7

Hasil perhitungan dari  adalah …

PEMBAHASAN :

Jawaban B

Soal No.8

Hasil perhitungan dari 75% :  adalah …

PEMBAHASAN :

Jawaban C

Soal No.9

Tentukan nilai 0,8 dari 200 kg adalah …

PEMBAHASAN 
Nilai pecahan dari suatu bilangan dapat ditentukan dengan cara mengalikan pecahan dengan bilangan tertentu.

0,8 dari 200 kg = x 200 kg =  x 200 kg =  = 160 kg
Jawaban A

Soal No.10

Hasil perhitungan dari 30%  x 0,2 :  adalah …

PEMBAHASAN :
Samakan bentuk pecahan-pecahan tersebut untuk memudahkan perhitungan.

Jawaban A

Soal No.11

Hasil perhitungan dari 0,25 x adalah …

PEMBAHASAN :
Samakan terlebih dahulu bentuk pecahannya, sebagai berikut:

Jawaban A

Soal No.12

Hasil perhitungan dari adalah …

PEMBAHASAN :
Untuk menyelesaikannya ubah pecahan campuran menjadi pecahan biasa, sebagai berikut:

Jawaban C

Soal No.13

Hasil perhitungan dari 421,72 + 102,524 adalah…

1. 424,102
2. 524,244
3. 511,144
4. 368,256

PEMBAHASAN :
Untuk menjumlahkan pecahan desimal, jumlahkan tiap angka sesuai nilai tempatnya yaitu puluhan lurus dengan puluhan, satuan lurus dengan satuan, koma lurus dengan koma, persepuluh lurus dengan persepuluh, dan perseratus lurus dengan perseratus.

421,72
102,524   +
524,244
Jawaban B

Soal No.14

Hasil perhitungan dari adalah …

PEMBAHASAN :
Pembagian pada bentuk pecahan dapat diselesaikan dengan mengalikan pecahan pertama  dengan pecahan kedua yang sudah dibalik posisinya (pertukaran pembilang menjadi penyebut dan penyebut menjadi pembilang). Dan untuk bentuk pecahan campuran, ubah terlebih dahulu menjadi pecahan biasa.

Jawaban D

Soal No.15

Beberapa bentuk pecahan berikut ini urutkan dari nilai yang terbesar yaitu:

0,45 ; 60% ; ;

1. 60% ; ; ; 0,45
2. ; 60% ; 0,45 ;
3. ; ; 60% ; 0,45
4. 60% ; ; 0,45 ; 

PEMBAHASAN :
Pada soal di atas bentuk pecahan belum sejenis. Untuk mengurutkan pecahan tersebut, ubah pecahan terlebih dahulu ke bentuk pecahan misalnya kebentuk desimal.

Maka urutan dari yang terkecil yaitu:; 60% ; 0,45 ;
Jawaban B

Soal No.16

Sebidang tanah dijual dengan harga Rp 35.000.000, 00 dengan memperoleh keuntungan sebesar 10%. Maka besar keuntungan yang diperoleh dari penjualan tanah tersebut adalah …

1. Rp 2.500.000,00
2. Rp 3.000.000,00
3. Rp 3.500.000,00
4. Rp 4.000.000,00

PEMBAHASAN :
Diketahui:
Harga jual tanah = Rp 35.000.000,00
Persentase keuntungan = 10%

Maka besar keuntungan yang diperoleh = persentase keuntungan x harga jual
= 10% x Rp 35.000.000,00
= x Rp 35.000.000,00

= Rp 3.500.000,00
Jawaban D

Soal No.17

Nisa memiliki kain sebanyak 10,5 meter. Kain tersebut akan dibagikan kepada Santi sebanyak 1,75 meter, Lena 2,0 meter, Rani 1,90 meter, dan Yanti 2,50 meter. Kemudian Nisa membeli lagi kain sebanyak 4,70 meter. Maka kain yang dimiliki Nisa saat ini adalah …

1. 7,05 meter
2. 6,75 meter
3. 8,00 meter
4. 5,90 meter

PEMBAHASAN :
Maka penyelesaian untuk soal di atas adalah:
Banyak kain yang dimiliki Nisa = 10, 5 – 1,75 – 2,0 – 1,90 – 2,50 + 4,70 = 7,05 meter
Jawaban C

Soal No.18

Pada proyek pemasangan listrik persediaan kabel sebanyak 12 meter akan digunakan di blok A sebanyak  meter, di blok B sebanyak  meter, dan di blok C sebanyak  meter. Maka kabel listrik yang tersisa adalah …

1. 0,6 meter
2. 0,7 meter
3. 0,8 meter
4. 0,9 meter

PEMBAHASAN :

Jawaban C

Soal No.19

Persediaan beras di suatu daerah untuk bantuan sembako tersisa 5,5 kg. Kemudian mendapat tambahan bantuan dari pemerintah pusat sebanyak 55,8 kg dan dari pemerintah daerah sebanyak 40,75 kg. Maka jumlah beras yang tersedia untuk disalurkan adalah sebanyak …

1. 100,35 kg
2. 102,05 kg
3. 88,75 kg
4. 97,52 kg

PEMBAHASAN :
Diketahui:
Persediaan beras = 5,5 kg
Tambahan dari pemerintah pusat = 55,8 kg
Tambahan dari pemerintah daerah = 40,75 kg
Maka total persediaan = 5,5 kg + 55,8 kg + 40,75 kg = 102,05 kg
Jawaban B

Soal No.20

Siswa-siswi di kelas 3A memiliki beberapa hobi yaitu 35% gemar sepak bola, 20% gemar basket, 32% gemar badminton, dan sisanya gemar bola voli. Maka persentase siswa/ siswi yang gemar bola voli adalah …

1. 21%
2. 17%
3. 12%
4. 13%

PEMBAHASAN :
Diketahui:
Gemar sepak bola = 35%
Gemar basket = 20%
Gemar badminton = 32%
Maka yang gemar bola voli = 100% – 35% – 20% – 32% = 13%
Jawaban D