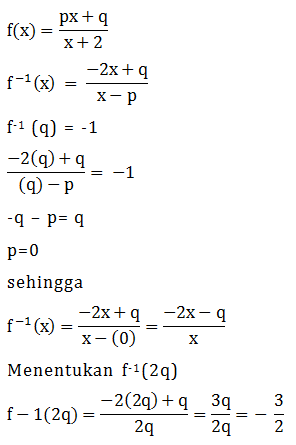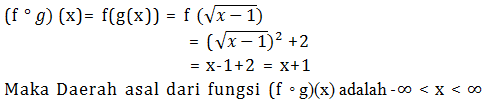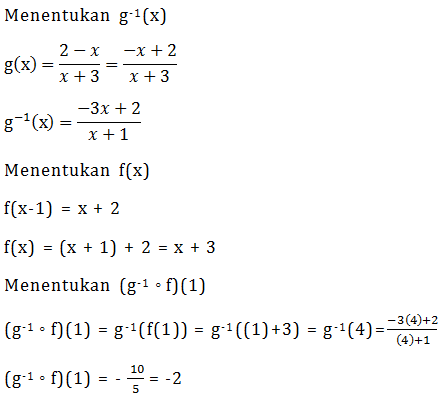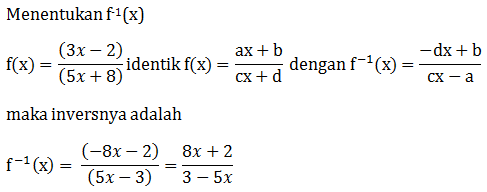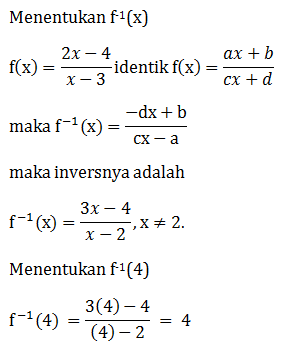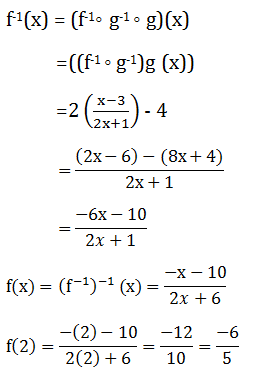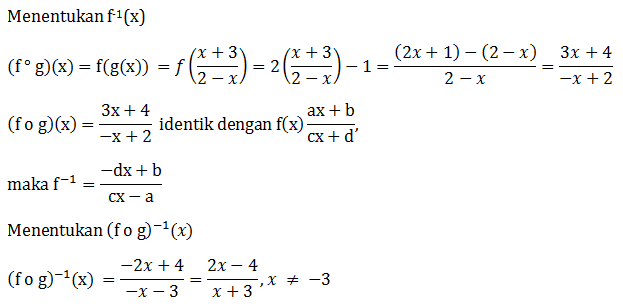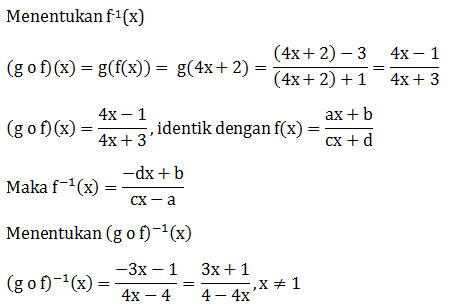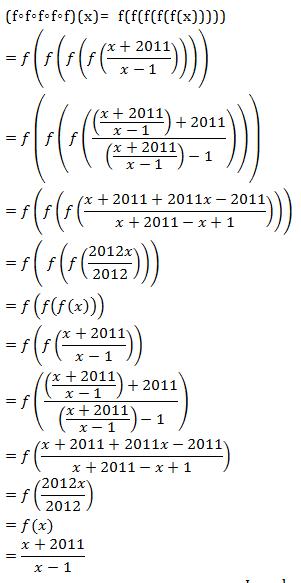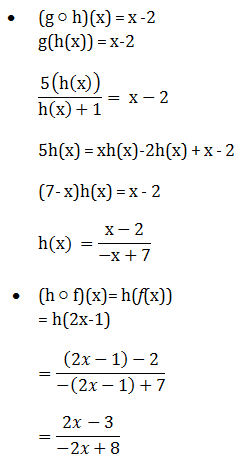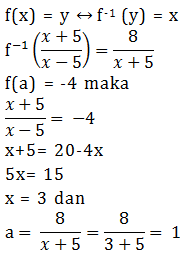Untuk Pembelajaran selanjutnya…
Ok kali ini kita akan membahas mengenai rangkuman materi dan contoh soal fungsi dan komposisi untuk kamu kelas 10 SMA. Kalau ingin mendalam memahami bab ini simak juga video pembelajaranya ada dua versi dari dua guru yang berbeda lho!. Ayo semangat belajar
Pengertian
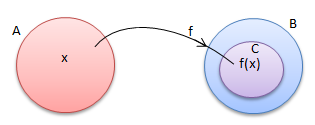
Fungsi merupakan relasi dua himpunan A dan B yang memasangkan setiap anggota pada himpunan A dengan tepat satu anggota himpunan B.
- himpunan A disebut domain (daerah asal),
- himpunan B disebut kodomain (daerah kawan)
- himpunan anggota B yangpasangan (himpunan C) disebut range (hasil) fungsi f.
Sifat-Sifat Fungsi
- Fungsi injektif (satu-satu)
Jika fungsi f : A → B, setiap b ∈ B hanya mempunyai satu kawan saja di A, contoh: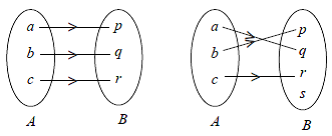
- Fungsi surjektif (onto)
Pada fungsi f : A → B, setiap b ∈ B mempunyai kawan di A.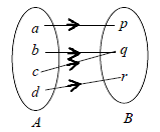
- Fungsi bijektif (korespondensi satu-satu)
Suatu fungsi yang bersifat injektif sekaligus surjektif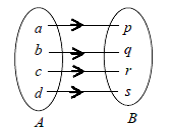
Aljabar Fungsi
- Penjumlahan f dan g
(f + g) (x) = f(x) + g(x).
Contoh Soal:
Diketahui f(x) = x + 2 dan g(x) = x2 – 4. Tentukan (f + g)(x).
Penyelesaian
(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2 - Pengurangan f dan g
(f – g)(x) = f(x) – g(x).
Contoh soal
Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).
Penyelesaian
(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1 - Perkalian f dan g
(f . g)(x) = f(x) . g(x).
Contoh soal
Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).
Penyelesaian
(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x - Pembagian f dan g

Contoh soal
Diketahui f(x) = x2 – 4 dan g(x) = x + 2. Tentukan
Penyelesaian
Fungsi Komposisi
Fungsi komposisi dapat ditulis sebagai berikut:
- (f ◦ g)(x) = f (g (x))→ komposisi g (fungsi f bundaran g atau fungsi komposisi dengan g dikerjakan lebih dahulu daripada f)

- (g ◦ f)(x)= g (f (x))→ komposisi f(fungsi g bundaran f atau fungsi komposisi dengan f dikerjakan lebih dahulu daripada g)
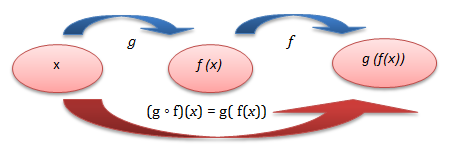
Sifat Fungsi Komposisi
- Tidak berlaku sifat komutatif, (f ◦ g)(x) ≠ (g ◦ f)(x).
- Berlaku sifat asosiatif, (f ◦(g ◦ h))(x) = ((f ◦ g)◦ h)(x).
- Terdapat unsur identitas (l)(x), (f ◦ l)(x) = (l ◦ f)(x) = f(x).
Contoh soal
Diketahui f(x) = 2x – 1, g(x) = x2 + 2.
- Tentukan (g ◦ f)(x).
- Tentukan (f ◦ g)(x).
- Apakah berlaku sifat komutatif: g ◦ f = f ◦ g?
Penyelesaian
- (g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3
- (f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3
- Tidak berlaku sifat komutatif karena g ◦ f ¹ f ◦ g.
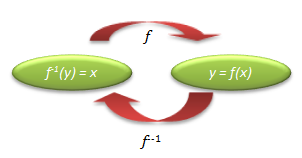
Fungsi Invers
- Menentukan fungsi invers : mengganti f (x)= y = …” menjadi “ f -1 (y)= x = …”
- hubungan sifat fungsi invers dengan fungsi komposisi:
- (f ◦ f-1)(x)= (f -1 ◦ f)(x)= l (x)
- (f ◦ g)-1 (x)= (g-1◦ f-1)(x)
- (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g -1)(x)
Versi 1
- Part 1
- Part 2
- Part 3
- Part 4
- Part 5
Versi 2
Soal No.1 (UTBK 2019)
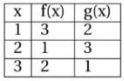
Diketahui grafik fungsi f’ dan g’ dengan beberapa nilai fungsi f dan g sebagai berikut
Jika h(x) = (fog)(x), maka nilai h'(2) adalah…
PEMBAHASAN :
h(x) = (fog)(x) = f(g(x))
h'(x) = g'(x).f'(g(x))
h'(2) = g'(2).f'(g(2))
Dengan melihat tabel fungsi f(x), g(x) serta kurva f'(x), g'(x), didapat:
g(2) = 3, g'(2) = 3, f'(3) = -3
Maka:
h'(2) = 3. f'(3) = 3. (-3) = -9
Jawaban B
Soal No.2 (UN 2012)
Diketahui fungsi g(x) = x + 1 dan f(x) = x2 + x – 1. Komposisi fungsi (f ◦ g)(x)= …
- x2 + 3x + 3
- x2 + 3x + 2
- x2 – 3x + 3
- x2 + 3x – 1
- x2 + 3x + 1
PEMBAHASAN :
Menentukan (f ◦ g)(x)
(f ◦ g)(x)= f (g (x)) = f (x + 1) = (x + 1)2 + (x + 1)- 1
(f ◦ g)(x)= x2 + 2x + 1 + x = x2 + 3x + 1
Jawaban : E
Soal No.3 (SBMPTN 2014 Dasar)
- -3
- -2


- 3
Soal No.4 (UN 2007)
Diketahui f : R → R, g : R → R dirumuskan oleh f(x) = x2 – 4 dan g(x) = 2x – 6. Jika (f ◦ g)(x)= -4 , nilai x = …
- -6
- -3
- 3
- 3 atau -3
- 6 atau -6
PEMBAHASAN :
Menentukan nilai x
(f ◦ g)(x) = -4
f(g (x)) = -4
f(2x – 6) = -4
(2x – 6)2 – 4 = -4
2x – 6 = 0
x = 3
Jawaban : C
Soal No.5 (SIMAK UI 2013 DASAR)
Diketahui f -1 (4x-5) = 3x-1 dan (f -1 ◦ f)(5)= p2 +2p – 10 maka rata-rata dari nilai p adalah…
- -4
- -2
- -1
- 1
- 4
PEMBAHASAN :
f (x) = y ↔ f -1 (y) = x
f (5) = y
f —1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
Menentukan nilai p
(f – -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
Jadi, rata-rata nilai p adalah ![]() = -1
= -1
Jawaban : C
Soal No.6 (UN 2003)
Ditentukan g (f(x)) = f(g(x)). Jika f(x)= 2x + p dan g(x) = 3x + 120 maka nilai p = …
- 30
- 60
- 90
- 120
- 150
PEMBAHASAN :
Menentukan nilai p
g (f (x)) = f (g (x))
g (2x + p) = f (3x + 120)
3 (2x + p) + 120 = 2 (3x + 120) + p
6x + 3p + 120 = 6x + 240 + p
2p = 120
p = 60
Jawaban : B
Soal No.7 (SPMB 2007 Dasar)
- -∞ < x < ∞
- 1 ≤ x ≤ 2
- x ≥ 0
- x ≥ 1
- x ≥ 2
Soal No.8 (UN 2013)
Diketahui fungsi f(x) = x – 4 dan g(x) = x2 – 3x + 7. Fungsi komposisi (g ◦ f)(x) = …
- x2 – 3x + 3
- x2 – 3x + 11
- x2 – 11x + 15
- x2 – 11x + 27
- x2 – 11x + 35
PEMBAHASAN :
Menentukan (g ◦ f)(x)
(g ◦ f)(x)= g (f (x)) = g (x – 4) = (x – 4)2 – 3(x – 4) + 7 = x2 – 8x + 16 – 3x + 12 + 7
(g ◦ f)(x) = x2 – 11x + 35
Jawaban : E
Soal No.9 (SIMAK UI 2012 DASAR)
Misalkan f : R→ R dan g : R→R, f(x) = x + 2 dan (g ◦ f)(x) = 2x2 + 4x – 6, Misalkan juga x1 dan x2 adalah akar-akar dari g(x) = 0 maka x1 + 2x2 =…
PEMBAHASAN :
Menentukan g(x)
(g ◦ f)(x) = 2x2 + 4x – 6
g(f(x)) = 2x2 + 4x – 6
g(x+2) = 2x2 + 4x -6
g(x) = 2(x – 2)2 + 4(x – 2) – 6 = 2x2 – 8x + 8 + 4x – 8 – 6 = 2x2 – 4x – 6
menentukan x1 + 2x2
g(x) = 0
2x2 – 4x – 6 = 0
x2 – 2x – 3 = 0
(x-3)(x+1) = 0
x1=3 →x2 = -1, jadi 3
x1 = 2x2 = 3+2 (-1) = 1
atau
x1 = -1 → x2 = 3, jadi
x1 + 2x2 = (-1) + 2(3) = 5
Jawaban : E
Soal No.10 (UN 2004)
Suatu pemetaan f:R→R dengan (g ◦ f)(x) = 2x2 + 4 x + 5 dan g(x) = 2x + 3. Maka f(x)=…
- x2 + 2x + 1
- x2 + 2x + 2
- 2x2 + x + 2
- 2x2 + 4x + 2
- 2x2 + 4x + 1
PEMBAHASAN :
Menentukan f(x)
(g ◦ f)(x) = 2x2 + 4x + 5
g(f(x)) = 2x2 + 4x + 5
2(f(x)) + 3 = 2x2 + 4x + 5
f(x) = x2 + 2x + 1
Jawaban : A
Soal No.11 (SNMPTN 2011 Dasar)


- 1
- 8
Soal No.12 (SNMPTN 2011 IPA)
- -6
- -2


- 4
Soal No.13 (UN 2008)
Soal No.14 (SNMPTN 2010 Dasar)
Jika g(x – 2) = 2x – 3 dan (f ◦ g)(x – 2) = 4x2 – 8x + 3, maka f(-3) =…
- -3
- 3
- 12
- 15
PEMBAHASAN :
g(x – 2) = 2x – 3
(f ◦ g)(x – 2) = 4x2 – 8x + 3
f(g(x – 2)) = 4x2 – 8x + 3
f(2x – 3) = 4x2 – 8x + 3
Menentukan f(-3)
Jika -3 = 2x – 3 maka x = 0
Sehingga:
f(-3) = 4(0)2 – 8(0) + 3 = 3
Jawaban : A
Soal No.15 (UN 2010)
- 4
- 6
- 8
- 10
Soal No.16 (SIMAK UI 2009 DASAR)
Soal No.17 (UN 2005)
- (f ◦ g)-1 =
 , x≠-3
, x≠-3 - (f ◦ g)-1 =
 , x≠-3
, x≠-3 - (f ◦ g)-1 =
 , x≠3
, x≠3 - (f ◦ g)-1 =
 , x≠-1
, x≠-1 - (f ◦ g)-1 =
 , x≠1
, x≠1
Soal No.18 (UM UGM 2010 DASAR)


- x – 2
- x – 3
- x + 5
Soal No.19 (UN 2014)
- (g◦f)-1 =
 , x ≠
, x ≠ 
- (g◦f)-1 =
 ,x ≠
,x ≠ 
- (g◦f)-1 =
 ,x ≠ -1
,x ≠ -1 - (g◦f)-1 =
 ,x ≠ 1
,x ≠ 1 - (g◦f)-1 =
 ,x ≠ -1
,x ≠ -1
Soal No.20 (SNMPTN 2011 Dasar)
Soal No.21 (UN 2005)
diketahui f : R →R, g : R → R, g(x) = 2x + 3 dan (f ◦ g)(x) = 12x2 + 32x + 26, Rumus f(x) =…
- 3x2 – 2x + 5
- 3x2 – 2x + 37
- 3x2 – 2x + 50
- 3x2 + 2x – 5
- 3x2 + 2x – 50
Soal No.22 (UM UGM 2009)
Diketahui f(x) = 2x – 1 dan g (x) = Jika h adalah fungsi sehingga (g ◦ h)(x) =x – 2 maka (h ◦ f)(x) = …
Soal No.23 (UN 2000)
Soal No.24 (SNMPTN 2013 Dasar)
- 2
- 1
- -1
- -2
Soal No.25 (UN 2000)
Diketahui fungsi f(x) = 2x + 1 dan (f ◦ g) (x+1)= -2x2 – 4x – 1. Nilai g(-2)=…
- -5
- -4
- -1
- 1
- 5
PEMBAHASAN :
Menentukan f(x)
f(x) = 2x + 1 → f(x + 1) = 2(x + 1) + 1 = 2x + 3
Menentukan g(-2)
(f ◦ g)(x + 1)= -2x2 – 4x – 1
f(g(x + 1)) = -2x2 – 4x – 1
2(g(x + 1)) + 3 = -2x2 – 4x – 1
g(x + 1) = -x2 – 2x – 2
Misal, x + 1 = -2 → x = -3
g(-2) = -(-3)2 – 2(-3) -2 = -5
Jawaban : A
Soal No.26 (SIMAK UI 2011 Dasar)




- 2
Soal No.27 (EBTANAS 1993)
Soal No.28 (EBTANAS 1991)
Fungsi f dan g ditentukan oleh f(x) = 2x-4 dan g(x) = ½ x + 3. Daerah asal f : {x| 2 ≤ x ≤ 6, x ∈ R) dan g :R→R. Daerah hasil dari (g ◦ f)(x) adalah…
- {y| 1 ≤ y ≤ 4, y ∈ R}
- {y| 4 ≤ y ≤ 6,y ∈ R}
- {y|3 ≤ y ≤ 7, y ∈ R}
- {y|-1 ≤ y ≤ 6, y ∈ R}
- {y|-1 ≤ y ≤ 17, y ∈ R}
PEMBAHASAN :
Menentukan (g ◦ f)(x)
(g ◦ f)(x) = g(f(x)) = g(2x-4) = ½ (2x-4)+3 = x + 1
Misal, y = (g ◦ f)(x)
Diketahui daerah asal f : {x| 2 ≤ x ≤ 6, x € R)
2 ≤ x ≤ 6
(2+1) ≤ (x+1) ≤ (6+1)
3 ≤ (g ◦ f)(x) ≤ 7
3 ≤ y ≤ 7, y ∈ R
Jawaban : C
Soal No.29
Jika diketahui fungsi :
Tentukan nilai dari f(-1) – f(1) + f(3)!
PEMBAHASAN :
Menentukan f(-1) dari y = f(x) = x + 2, untuk -3 ≤ x ≤ 0
f(-1) = (-1) + 2 = 1
Menentukan f(1) dan f(3) dari y = f(x) = x2 + 2, untuk 0 ≤ x ≤ 3
f(1) = (1)2 + 2 = 3
f(3) = (3)2 + 2 = 11
Maka:
f(-1) – f(1) + f(3) = 1 – 3 + 11 = 9
Soal No.30
Jika diketahui fungsi f(x) = x2 – 2x + 2. Jika f(n) = 10 tentukan nilai n yang memenuhi
PEMBAHASAN :
f(n) = 10 → n2 – 2n + 2 = 10
n2 – 2n – 8 = 0
(n – 4)(n + 2)
Maka nilai n yang memenuhi adalah 4 dan -2
Soal No.31
Jika diketahui fungsi f(x) = 5x. Untuk setiap x berlaku f(x + 2) – f (x) = ….
- 6.f(x)
- 12.f(x)
- 18.f(x)
- 22.f(x)
- 24.f(x)
PEMBAHASAN :
Diketahui:
f(x) = 5x
Maka:
f(x -1) + f (x) = 5x+2 – 5x
. = 5x . 52 – 5x
. = 25. 5x – 5x
. = 24.5x
. = 24.f(x)
Jawaban E
Soal No.32
Tentukan domain/daerah asal dari fungsi berikut


- f(x) = 2log(x2 + 5x – 14)
- f(x) = (x-2)log(x + 2)
PEMBAHASAN :
Demikian pembahasan kita mengenai rangkuman materi dan contoh soal fungsi dan komposisi. Kalau bermanfaat buat kamu bantu kita juga yah untuk share dan beritahu teman kamu untuk berkunjung ke artikel ini. Terima kasih
Semoga Bermanfaat