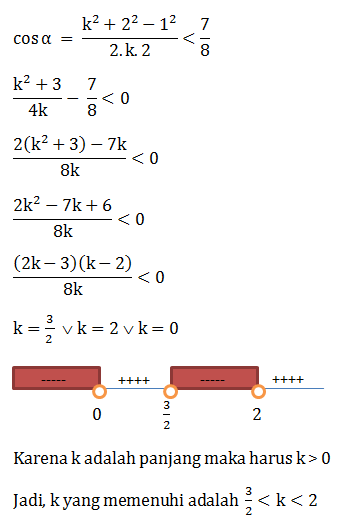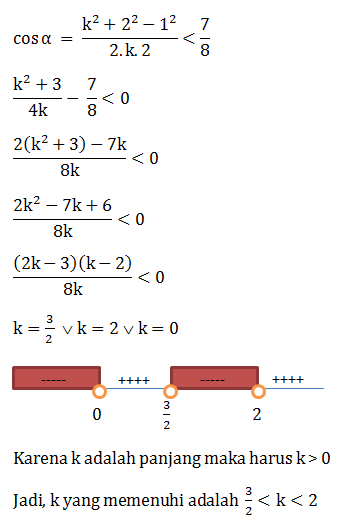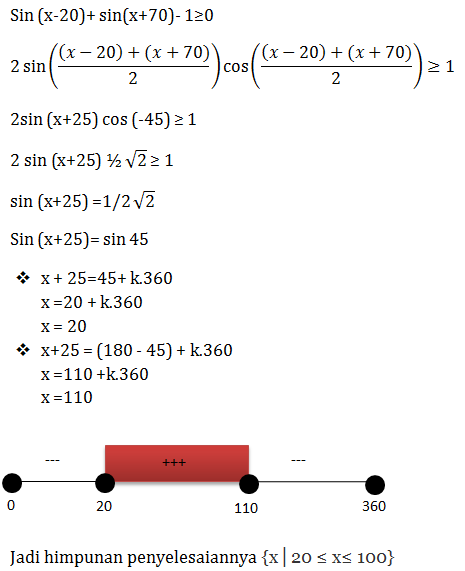Untuk Pembelajaran selanjutnya…
Diketahui cos x = 3/5 untuk 0o < x < 90o. Nilai dari sin 3x + sin x = …..
Pada segitiga ABC diketahui 3 sin A+ 4 cos B = 6 dan 3 cos A + 4 sin B = 1 Nilai sin C = ….
Diketahui sin(x – 60⁰ ) + sin(x + 60⁰) = p. Hasil dari sin 2x = …
Dalam segitiga ABC, diketahui sudut α,β, γ berhadapan dengan sisi a, b, c, . Jika b>c maka:
Himpunan peneyelesaian persamaan sin2 2x-2 sin x cos x -2 = 0, untuk 0 ≤ x ≤ 3600 adalah
Nilai cos x – √3 sin x >0 , jika..
himpunan penyelesaian persamaan cos 2x – 3 cos x + 2 = 0 untuk 0 ≤ x ≤ 2π adalah…
Soal No.31 (UN 2001)
Himpunan penyelesain dari sin (x-20) + sin (x+70) – 1 ≥0 untuk 0 ≤ x ≤ 360 adalah……
- {x│20 ≤ x≤ 100}
- {x│ 35 ≤ x ≤ 100}
- {x│ x≤ 50 atau x ≥ 130}
- {x│≤ 35 atau x≥ 145}
- {x│x ≤ 50 atau x ≥ 310}
Soal No.32 (SIMAK UI 2011)
Nilai-nilai x, untuk 0o ≤ x ≤ 360° yang memenuhi sin x + sin 2x > sin 3x adalah …
- 0° < x < 120°, 180° < x < 240°
- 0° < x < 150°, 180° < x < 270°
- 120° < x < 180°, 240o < x < 360°
- 150° < x < 180°, 270° < x < 360°
- 0° < x < 135°, 180° < x < 270°
Soal No.33
PEMBAHASAN :
Jawaban : B
Soal No.34
PEMBAHASAN :
Jawaban : A
Soal No.35
Diketahui ΔPQR siku-siku di Q, ∠P = x, ∠R = x, dan PR = 60, maka keliling ΔPQR = …
- 30(1 –
 )
) - 90(1 + 2
 )
) - 30(2 –
 )
) - 60(1 +
 )
) - 20(3 + 2
 )
)
PEMBAHASAN :
∠P + ∠R = 90
x + x = 90
2x = 900
x = 45![]()
PQ = PR . sin x
. = 60 . sin 45
. = 60 . ½![]()
. = 30![]()
![]()
QR = PR . cos x
. = 60 . cos 450
. = 60 . ½![]()
. = 30![]()
Maka keliling ΔPQR dapat dihitung sebagai berikut:
K ΔPQR = PQ + PR + QR
. = 30![]() + 60 + 30
+ 60 + 30![]()
. = 60 + 60![]()
. = 60(1 + ![]() )
)
Jawaban : D
Soal No.36
Jika θ = 3/2, maka ¼ sin θ cos θ – tan θ adalah …
- ½
- -1/3
- -¼
- -½
- 1/5
PEMBAHASAN :
θ = 3/2
θ = 3/2 x 180 = 270
sin 270 = sin (180 + 90) = 0 + 1 = 1
cos 270 = cos (180 + 90) = -1 + 0 = -1
tan 270 = tan (180 + 90) = 0
Maka ¼ sin θ cos θ – tan θ = ¼ sin 270 cos 270 – tan 270
. = ¼ . 1 . -1 – 0 = -¼
Jawaban : C
Soal No.37
Diketahui bujur sangkar ABCD dengan panjang diagonal 4p berpotongan di titik O, X terletak pada OC, dan OX = ½OC. Maka sin ∠XBO adalah …
PEMBAHASAN :
Diagonal bidang AC = BD = 4p![]()
OB = ½ BD = ½ . 4p![]() = 2p
= 2p![]()
OX = ½ OC = AC = . 4p![]() = p
= p![]()

Maka sin ∠XBO dapat dihitung sebagai berikut:
Jawaban : E
Soal No.38
Sin2 (20) + sin2 (50) + sin2 (70) + sin2 (40) = …
- 1
- 2
- 3
- 4
- 5
PEMBAHASAN :
Berlaku sin2 a + cos2 a = 1
Sin 20 = sin (90 – 700 ) = cos 70
Sin 500 = sin (90 – 40) = cos 40
Maka soal di atas dapat diselesaikan sebagai berikut:
Sin2 (20) + sin2 (50) + sin2 (70) + sin2 (40)
= Cos2 (700 ) + cos2 (40) + sin2 (70) + sin2 (40)
= {Cos2 (700 ) + sin2 (70)} + { cos2 (40) + sin2 (40)}
= 1 + 1
= 2
Jawaban : B
Soal No.39
Diketahui sin α + cos α = 2, maka sin3 α + cos3 α = …
- 11
- 20
- 13
- 17
- 25
PEMBAHASAN :
Berlaku sin2 α + cos2 α = 1
Misalkan:
p = sin α
q = cos α
p + q = 2
(p + q)2 = 4
P2 + 2pq + q2 = 4
(p2 + q2) + 2pq = 4
1 + 2pq = 4
2pq = 3
pq = 3/2
Maka sin3 α + cos3 α
= p3 + q3
= (p + q)3 + 3p2q + 3pq2
= (p + q)3 + 3pq(p + q)
= 23 + 3.3/2(2)
= 8 + 9
= 17
Jawaban : D
Soal No.39
Diketahui ΔABC dengan AB = 100 cm, ∠A = 600 , ∠B = 750 , dan ∠C = 450 . Maka Panjang BC adalah …
PEMBAHASAN :

Jawaban : A
Soal No.40
PEMBAHASAN :
Jawaban : E
Soal No.41
- 1 – sin x
- 1 + tan x
- 1 + cos x
- ½ – sin x
- ½ – cos x
PEMBAHASAN :
Jawaban : C
Soal No.42
Diketahui sebuah lingkaran memiliki panjang jari-jari 10 cm yang dibuat segi enam beraturan. Maka panjang sisi segi enam tersebut adalah …
- 10 cm
- 6 cm
- 13 cm
- 8 cm
- 11 cm
PEMBAHASAN :![]()
Maka panjang sisi segi enam beraturan tersebut dapat dihitung sebagai berikut:
Misalkan:
Panjang sisi = a
Jawaban : B
Soal No.43
Terdapat ΔABC dengan a = 3, b = 3, dan c = 4. Maka cos A = …
PEMBAHASAN :
Diketahui:
a = 3
b = 3
c = 4
Jawaban : A
Soal No.44
Diketahui luas ΔPQR = 20 cm2 , panjang PR = 10 cm, dan panjang PQ = 8 cm. Maka cos ∠RPQ adalah …
PEMBAHASAN :
Luas ΔPQR = ½ . PR . PQ . sin ∠RPQ
20 = ½ . 10 . 8 . sin P
20 = 40
Sin ∠RPQ = ![]()
∠RPQ = 30
Maka cos ∠RPQ = ½![]()
Jawaban : D
Soal No.45
Sebuah segitiga dengan titik-titik sudut (-6,0), (6,0), dan (6 cos α, 6 sin α). Banyak nilai α yang mungkin agar luas segitiga tersebut 12 adalah … (0 ≤ x ≤ 2p).
- 1
- 2
- 3
- 4
- 5
PEMBAHASAN :
Luas Δ = ½ . alas . tinggi
12 = ½ . 12 . 6 sin α
12 = 36 sin α

Maka terdapat 4 nilai a pada segitiga tersebut
Jawaban : D
Soal No.46
- ¼
 (1 –
(1 –  )
) - ½
 (1 +
(1 +  )
) - ¼ (
 –
–  )
) - 2
 (1 +
(1 +  )
)  (1 –
(1 –  )
)
PEMBAHASAN :
tan a = ![]() , a = 30
, a = 30
tan b = 1 , b = 45
sin a = ½
cos a = ½ ![]()
sin b = ½![]()
cos b = ½ ![]()
sin (a – b) = sin a . cos b – cos a . sin b
= ½ . ½ ![]() – ½
– ½ ![]() . ½
. ½ ![]()
= ¼ ![]() – ¼
– ¼ ![]()
= ¼ ![]() (1 –
(1 – ![]() )
)
Jawaban : A
Soal No.47
PEMBAHASAN :
Diketahui
cos ∠A = ![]()
→ sin ∠A = ![]()
cos ∠B = ![]()
→ sin ∠B = ![]()
Maka sin ∠C dapat dihitung sebagai berikut:
Sin ∠C = sin {1800 – (A + B)}
= sin (A + B)
= (sin A . cos B) + (cos A . sin B)
Jawaban : B
Soal No.48
Hasil perhitungan dari cos 250 cos 350 – sin 250 sin 350 = …
- 30
- 40
- 500
- 60
- 90
PEMBAHASAN :
cos 250 cos 350 – sin 250 cos 350
= cos (250 + 35)
= cos 60
= cos (900 – 60)
= sin 30
Jawaban : A
Soal No.49
Jika α – β = ½ π, sin α . sin β = 1/3, dan α dan β adalah sudut lancip. Maka nilai cos (α + β) = …
PEMBAHASAN :
α – β = ½ π
Cos (α – β) = cos ½ π
Cos α cos β + sin α . sin β = ½
Cos α cos β + ![]() = ½
= ½
Cos α cos β = ![]()
cos (α + β) = Cos α cos β – sin α . sin β
Jawaban : E
Soal No.50
PEMBAHASAN :
Diketahui:
sin α – sin β = ![]()
cos α + cos β = ![]()
Persamaan 1:
sin α – sin β = ![]() (kuadratkan)
(kuadratkan)
sin2 α – 2 sin α sin β + sin2 β = P
Persamaan 2:
cos α + cos β = ![]() (kuadratkan)
(kuadratkan)
cos2 α + 2 cos α cos β + cos2 β = Q
Berlaku:
sin2 x + cos2 x = 1
Jumlahkan persamaan 1 dan 2 sebagai berikut:
(sin2 α + cos2 α) + 2(cos α cos β – sin α sin β) + (sin2 β + cos2 β) = P + Q
1 + 2(cos α cos β – sin α sin β) + 1 = P + Q
2 + 2 cos (α + β) = P + Q
Cos (α + β) = ![]()
Jawaban : B
Soal No.51
PEMBAHASAN :
Jawaban : E
Soal No.52
PEMBAHASAN :
Jawaban : A
Soal No.53
Hasil perhitungan dari 2 sin 300 cos 300 adalah …


-


- 1
PEMBAHASAN :
2 sin α cos β = sin (α + β) + sin (α – β)
2 sin 300 cos 300 = sin (300 + 30) + sin (300 – 30)
2 sin 300 cos 300 = sin 600 + sin 0
2 sin 300 cos 300 = ![]() + 0
+ 0
2 sin 300 cos 300 = ![]()
Jawaban : D
Soal No.54
Bentuk sederhana dari trigonometri 5 sin A sin B adalah …
- – sin B
- – 5 cos B
- sin A + sin B
- sin A – sin B
- cos (A + B)
PEMBAHASAN :
5 sin A sin B = 5 x ½ {cos (A – B) – cos (A + B)}
5 sin A sin B = 5 x ½ (cos A – cos B – cos A – cos B)
5 sin A sin B = 5 x ½ (- 2 cos B)
5 sin A sin B = – 5 cos B
Jawaban : B
Soal No.55
Hasil perhitungan dari sin 900 + sin 300 = …
PEMBAHASAN :
sin 900 + sin 300 = 2 sin ½ (900 + 300 ) . cos ½ (900 – 30)
sin 900 + sin 300 = 2 sin ½ (120) . cos ½ (60)
sin 900 + sin 30 = 2 sin 600 . cos 30
sin 900 + sin 300 = 2 .![]() .
. ![]()
sin 900 + sin 300 = ![]()
Jawaban : A
Soal No.56
PEMBAHASAN :
Berlaku:
Sin 2α = 2 sin α cos α
Segitiga dengan tipe teorema Pythagoras, maka cos α = ![]()
Sin 2α = 2 sin α cos α
Sin 2α = 2 . ![]() .
. ![]()
Sin 2α =![]()
Jawaban : E
Soal No.57
PEMBAHASAN :
Jawaban : D
Soal No.58
Diketahui P, Q, R adalah sudut-sudut ΔPQR dengan P – Q = 600 dan sin C = 2/3. Maka sin P cos Q = …
PEMBAHASAN :
Sin P cos Q = ½ {sin (P + Q) + sin (P – Q)}
Sin P cos Q = ½ {sin (1800 – C) + sin 600 }
Sin P cos Q = ½(sin C +![]() )
)
Sin P cos Q = ½(![]() +
+![]() )
)
Sin P cos Q =![]()
Jawaban : C
Soal No.59
Nilai dari cot 900 . tan 300 = …
- 1
- ½


PEMBAHASAN :
Jawaban : A
Soal No.60
Nilai x dari persamaan sin 2x – sin x = 0 (00 ≤ x ≤ 3600 ) adalah …
- 0 dan 300
- 0 dan 600
- 200 dan 500
- 300 dan 45
- 450 dan 90
PEMBAHASAN :
sin 2x – sin x = 0
2 sin x cos x – sin x = 0
sin x (2 cos x – 1) = 0
sin x = 0 → x = 0
2 cos x – 1 = 0
2 cos x = 1
cos x = ½ → x = 60
Jawaban : B
Soal No.61
Jika cos 2x – cos x = 2 dengan 00 ≤ x ≤ 3600 . Maka nilai x yang memenuhi adalah …
- 90
- 60
- 120
- 270
- 180
PEMBAHASAN :
(2 cos2 x – 1) – cos x – 2 = 0
2 cos2 x – cos x – 3 = 0
Misalkan:
cos x = a
Berlaku:
-1 ≤ cos x ≤ 1
Maka 2 cos2 x – cos x – 3 = 0 → 2a2 – a – 3 = 0
(2a – 3)(a + 1) = 0
2a – 3 = 0
2a = 3
a = 3/2 (tidak memenuhi)
a + 1 = 0
a = – 1 (memenuhi)
cos x = – 1
x = 180
Jawaban : E
Soal No.62
- 1350 dan 225
- 900 dan 270
- 1800 dan 180
- 1500 dan 210
- 1200 dan 240
PEMBAHASAN :![]() + 2 cos x = 0
+ 2 cos x = 0
2 cos x = – ![]()
cos x = – ½ ![]()
x1 = 1500
x2 = 210
Jawaban : D
Soal No.63
PEMBAHASAN :
Jawaban : C
Soal No.64
- 30
- 60
- 90
- 120
- 150
PEMBAHASAN :
Jawaban : A
Soal No.65
- {450 , 1350 , 2250 , 3150 }
- {300 , 600 , 1800 , 2700 }
- {600 , 1200 , 1800 , 2400 }
- {00 , 450 , 1350 , 2250 }
- {900 , 1800 , 2700 , 3600 }
PEMBAHASAN :![]()
![]() → kalikan cos x
→ kalikan cos x
2 cos2 x – 2![]() cos x + 1 = 0
cos x + 1 = 0
( ![]() cos x – 1)2 = 0
cos x – 1)2 = 0
( ![]() cos x – 1) (
cos x – 1) (![]() cos x – 1) = 0
cos x – 1) = 0![]() cos x – 1 = 0
cos x – 1 = 0
cos x = ± ½ ![]()
kuadran I → x = 45
kuadran II → x = 1350
kuadran III → x = 225
kuadran IV → x = 315
Jawaban : A
Soal No.66
Nilai-nilai x yang memenuhi 4 cos4 x – 4 cos2 x = 0 dengan 0 ≤ x ≤ ½π adalah …
- 30 dan 60
- dan 90
- 45 dan 45
- 60 dan 120
- 90 dan 90
PEMBAHASAN :
4 cos4 x – 4 cos2 x = 0
4 cos2 x (cos2 x – 1) = 0
4 cos2 x = 0
cos x = 0
x = 90
cos2 x – 1 = 0
cos x = 1
x = 0
Jawaban : B
Soal No.67
- 1
- – ½
- – 1
- 2
PEMBAHASAN :
Berlaku:
y = a sin kx + c
nilai y minimum = – |a|+ c
f(x) = 3 sin (x – ![]() ) + 2
) + 2
a = 3
c = 2
Maka nilai y minimum = – |3|+ 2 = – 1
Jawaban : D
Soal No.68
- {x|67,50 ≤ x ≤ 112,5}
- {x|1350 ≤ x ≤ 225}
- {x|900 ≤ x ≤ 120}
- {x|450 ≤ x ≤ 125}
- {x|300 ≤ x ≤ 150}
PEMBAHASAN :
2 cos 2x0 + ![]() ≤ 0
≤ 0
cos 2x = -½![]()
2x = 135 dan 225
x = 67,5 dan 112,5
Maka nilai yang memenuhi 67,50 ≤ x ≤ 112,5
Jawaban : A
Soal No.69
Nilai x yang memenuhi persamaan sin (x + 60) + cos (x + 60) = 0 dengan 0 ≤ x ≤ 3600 adalah …
- {600 , 300}
- {1200 , 240}
- {900 , 270}
- {1800 , – 180}
- {- 900 , – 270}
PEMBAHASAN :
sin (x + 600 ) + cos (x + 60) = 0
sin (x + 600 ) = – cos (x + 60)
berlaku:
cos x = sin (x – 90) atau sin(x + 90)
tan (x + 60) = tan 150
x + 600 = 1500 ± k.180
x = 900 ± k.180
k = 0 → x = 900 (memenuhi)
k = 1 → x = – 900 (tidak memenuhi) atau x = 2700 (memenuhi)
k = 2 → x = – 2700 (tidak memenuhi) atau 4500 (tidak memenuhi)
Maka himpunan penyelesaiannya = {900 , 270}
Jawaban : C
Soal No.70
Perhatikan grafik berikut ini!

Persamaan untuk grafik di atas adalah …
PEMBAHASAN :
Jawaban : E
Soal No.71
Perhatikan kurva pada grafik berikut ini!

Persamaan grafik fungsi pada gambar adalah …
- y = 2 cos (2x – 20o)
- y = 2 cos (x – 20o)
- y = 2 cos (2x – 10o)
- y = 2 cos (x – 10o)
- y = 2 cos (2x – 40o)
PEMBAHASAN :
Jawaban : A
Soal No.72
Perhatikan kurva pada grafik berikut ini!

Persamaan yang sesuai dengan kurva di atas adalah …
PEMBAHASAN :
Bentuk umum persamaan kurva pada grafik di atas adalah y = 2 sin x. Kurva tersebut bergeser ke kiri sejauh ![]() . Maka persamaannya menjadi:
. Maka persamaannya menjadi:![]()
Jawaban : B
Soal No.73
Nilai minimum dari f(x) = 3 sin (x – π/4) + 2 adalah …
- -1
- 1
- 2
- 3
PEMBAHASAN :
Bentuk umum dari persamaan tersebut adalah y = a sin kx + c
a = 3
c = 2
Untuk menghitung nilai y minimum sebagai berikut:
Nilai minimum = – |a|+ c = – 3 + 2 = – 1
Jawaban : A
Soal No.74
- 10
- 14
- 16
- 20
- 30
PEMBAHASAN :
F(x) = ![]() cos 2x + 2
cos 2x + 2
a = ![]()
c = 2
Nilai maksimum F(x) = p = |a| + c = ![]() + 2
+ 2
Nilai minimum F(x) = q = – |a| + c = –![]() + 2
+ 2
Maka:
p2 + q2 = (![]() + 2 )2 + (-
+ 2 )2 + (-![]() + 2 )2
+ 2 )2
(3 + 4![]() + 4 ) + (3 – 4
+ 4 ) + (3 – 4![]() + 4 )
+ 4 )
= 14
Jawaban : B
Soal No.75
- 20
- 18
- 28
- 32
- 40
PEMBAHASAN :
Jawaban : D
Soal No.76
Nilai maksimum dan minimum dari y = 8 sin x + 6 cos x + 12 secara berturut-turut adalah …
- 10 dan 5
- 12 dan 4
- 22 dan 2
- 18 dan 8
- 26 dan 10
PEMBAHASAN :
Jawaban : C
Soal No.77
- 1050 dan 345
- 900 dan 1800
- 450 dan 135
- 1200 dan 240
- 750 dan 225
PEMBAHASAN :![]() sin x +
sin x + ![]() cos x = 1
cos x = 1
Kalikan persamaan di atas dengan ½, sehingga:
½![]() sin x + ½
sin x + ½![]() cos x = ½
cos x = ½
sin 450 sin x + cos 450 cos x = cos 600
cos (x – 45) = cos 60
Maka diperoleh:
x – 450 = ± 600 + k . 360
x1 – 450 = 600 + k . 3600
x1 = 1050 + k . 360
k = 0 → x1 = 1050 + k . 3600 → x1 = 1050 + 0 . 360 = 1050 (memenuhi)
k = 1 → x1 = 1050 + k . 3600 → x1 = 1050 + 1 . 3600 = 4650 (tidak memenuhi)
x2 – 450 = – 600 + k . 360
x2 = – 150 + k . 360
k = 0 → x2 = – 150 + k . 3600 → x2 = – 150 + 0 . 3600 = – 150 (tidak memenuhi)
k = 1 → x2 = – 150 + k . 3600 → x2 = – 150 + 1 . 3600 = 3450 (memenuhi)
Jawaban : A
Soal No.78
Himpunan penyelesaian dari tan (30 – ½ x)0 = cot (x + 60)0 dengan 0 ≤ x ≤ 3600 adalah …
- {600 , 300}
- {450 , 180}
- {00 , 360}
- {00 , 90}
- {1200 , 240}
PEMBAHASAN :
tan (30 – ½ x)0 = cot (x + 60)
tan (30 – ½ x)0 = tan (90 – (x + 60))
tan (30 – ½ x)= tan (- x + 30)
300 – ½ x = – x + 300 + k . 180
x – ½ x = k . 180
½ x = k . 180
x = k . 360
k = 0 → x = k . 3600 → x = 0
k = 1 → x = 1 . 3600 → x = 360
Maka Hp = {00 , 360}
Jawaban : C
Semoga Bermanfaat