100 Soal TIU SKD CPNS 2019 No. 41

By Posted on

pembahasan selanjutnya adalah

Tes CPNS berbasis CAT, 100 Soal TIU SKD CPNS 2019 No. 41 - 50 [Soal dan Pembahasan]

Pembahasan Simulasi Computer Assisted Test (CAT) bidang Tes Intelegensi Umum (TIU) Seleksi Kompetensi Dasar (SKD) CPNS 2019 nomor 41 sampai dengan nomor 50.

Soal No. 41

Pardi mempunyai 48 karung gula di tokonya dengan berat masing-masing karung adalah sama. Pardi kemudian mengirim 3/8 gulanya ke Toko Cilincing dan 2/5 gulanya ke Toko Papaho. Jika di toko Pardi masih tersedia 1728 kg gula, berapa berat setiap karung semula?



Pembahasan

Beras yang dikirim Pardi ke Toko Cilincing dan Toko Papaho adalah:

Bagian beras yang dikirim Pardi ke Toko Cilincing dan Toko Papaho, soal TIU cpns 3/5+2/5=31/40

Ini berarti sisa beras di tokonya adalah:

Sisa beras di toko Pardi dalam karung, soal TIU skd cpns

10,8 karung tersebut berisi 1728 kg, sehingga:

10,8 karung = 1728 kg
1 karung = 1728 : 10,8 kg
= 160 kg

Jadi, berat setiap karung adalah 160 kg (B).

Soal No. 42

NASABAH : PRIVASI = ….
A. pelanggan : kenyamanan
B. akuntan : kesalahan
C. perampok : buron
D. pejabat : jabatan
E. polisi : tilang

Pembahasan

Kata hubung yang tepat pada soal di atas adalah berhak mendapatkan.

NASABAH : PRIVASI
(NASABAH berhak mendapatkan PRIVASI)

pelanggan : kenyamanan
(pelanggan berhak mendapatkan kenyamanan)

Jadi, jawaban yang tepat adalah opsi (A).

Soal No. 43

Setiap kelinci pandai melompat.
Semua kelinci makan rumput.
A. Ada kelinci yang tidak pandai melompat.
B. Kelinci putih tidak makan rumput.
C. Semua kelinci makan rumput pandai melompat.
D. Ada kelinci yang pandai melompat tidak makan rumput.
E. Tidak ada kelinci yang pandai melompat.

Pembahasan

Diagram Venn untuk soal di atas adalah:

Diagram Venn kelinci, pandai melompat, makan rumput, soal TIU skd cpns

Jadi, penarikan kesimpulan yang tepat adalah semua kelinci makan rumput dan pandai melompat (C).

Soal No. 44

Dalam rangka menyemarakkan hari jadi kota Langka diadakan lomba lari. Ani, Budi, Cintia, Dadang, Ema, dan Farhan adalah peserta lomba tersebut. Dadang lebih cepat daripada Ema. Farhan tidak lebih cepat daripada Cintia, namun ia lebih cepat jika dibandingkan dengan Budi. Ema memiliki kecepatan yang hampir setara dengan Ani sehingga Ani selalu berada tepat di belakang Ema.
Artkel Terkait  Rangkuman Materi, Contoh Soal Puisi Lama Jawaban & Pembahasannya

Setelah lomba selesai semua peserta diberi label nomor 1 hingga 6 yang menandakan bahwa nomor 1 adalah yang tercepat dan sebaliknya. Tidak ada anak yang kecepatan larinya sama.

Jika Cintia selalu tepat di depan Ema maka urutan yang benar dimulai dari yang paling cepat adalah ….

A. Cintia – Ema – Ani – Dadang – Farhan – Budi
B. Dadang – Cintia – Ema – Farhan – Budi – Ani
C. Cintia – Ema – Dadang – Ani – Farhan – Budi
D. Dadang – Budi – Cintia – Ema – Ani – Farhan
E. Dadang – Cintia – Ema – Ani – Farhan – Budi

Pembahasan

Soal tipe seperti ini (menentukan urutan), lebih praktis dibandingkan langsung antara ketentuan soal dengan opsi jawaban.

  • Dadang lebih cepat daripada Ema. [opsi A dan C salah]
  • Farhan lebih cepat jika dibandingkan dengan Budi. [opsi D salah]
  • Ani selalu berada tepat di belakang Ema. [ops B dan C salah]

Jadi, urutan yang benar dimulai dari yang paling cepat adalah opsi (E).

Soal No. 45

5, 7, 12, 19, 31, 50, ….
A. 81, 131
B. 81, 121
C. 71, 121
D. 71, 131
E. 131, 181

Pembahasan

Perhatikan pembentukan pola barisan bilangan berikut ini!

Pola barisan bilangan 5, 7, 12, 19, 31, 50, …., soal TIU CPNS

Ini mirip barisan bilangan Fibonacci. Bedanya, pada barisan Fibonacci suku pertama sama dengan suku kedua.

Jadi, dua suku berikutnya dari barisan bilangan tersebut adalah 18 dan 131 (A).

Soal No. 46

Indah berjalan ke arah utara sejauh 500 cm, kemudian berjalan ke barat sejauh 12 m. Jarak posisi Indah saat ini dari posisi awal adalah … m.

Pembahasan

Perhatikan ilustrasi berikut ini!

Artkel Terkait  Download Soal SBMPTN TKD SAINTEK Tahun 2018

Indah berjalan ke utara 500 cm, kemudian ke barat 12 m, soal TIU skd cpns

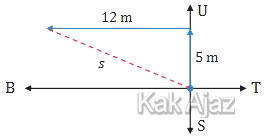
s adalah jarak posisi awal dan akhir yang bisa dicari dengan hukum Pythagoras sebagai berikut:

Jarak posisi Indah dari posisi awal, soal TIU skd cpns

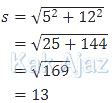
Jadi, jarak posisi Indah saat ini dari posisi awal adalah 13 m (A).

Tips:

Disarankan hafal triple Pythagoras berikut ini:

Pada soal di atas, tersaji angka 500 cm (5 m) dan 12 m. Jika hafal triple Pythagoras, maka angka satunya lagi adalah 13.

Dengan demikian, soal di atas langsung bisa terjawab hanya dengan pandangan mata.

Soal No. 47

123, 147, 223, 171, ….
A. 323, 195
B. 323, 205
C. 333, 205
D. 346, 194
E. 343, 215

Pembahasan

Perhatikan pola pembentukan barisan bilangan berikut!

Pola barisan bilangan 123, 147, 223, 171, …., soal TIU skd cpns

Jadi, dua suku berikutnya adalah 323 dan 195 (A).

Soal No. 48

Jawa Tengah : Semarang = Malaysia : ….
A. Kuching
B. ASEAN
C. Serawak
D. Kuala Lumpur
E. Kalimantan

Pembahasan

Kata penghubung yang tepat untuk soal di atas adalah ibukota-adalah.

Jawa Tengah : Semarang = Malaysia : Kuala Lumpur
(Ibukota Jawa Tengah adalah Semarang sebagaimana ibukota Malaysia adalah Kuala Lumpur)

Jadi, jawaban yang tepat adalah Kuala Lumpur (D).

Soal No. 49

Data 5, 2, 3, 5, 10, 8, 12, 10, a, b memiliki modus 5 dan median 6. Berapa banyak data yang nilainya di bawah rata-rata ….

Pembahasan

Data setelah diurutkan adalah sebagai berikut:

2, 3, 5, 5, 8, 10, 10, 12, a, b

Karena modus = 5 maka angka 5 harus muncul paling banyak (3 kali) sehingga a = 5 dan menempati data ke-5.

Sementara itu, median = 6. Hal ini berarti pertengahan data ke-5 dan ke-6 harus sama dengan 6. Sehingga b = 7.

Rata-rata data tersebut adalah:

Nilai rata-rata dari 10 data, jumlah data = 67, banyak data = 10, rataan = 6,7

Dengan demikian, nilai di bawah rata-rata adalah:

2, 3, 5, 5, 5 (5 data)

Artkel Terkait  Pembahasan TWK SKD CPNS 2019 No. 11

Jadi, banyak data yang nilainya di bawah rata-rata adalah 5 (A).

Soal No. 50

Jika jumlah 101 bilangan kelipatan tiga yang berurutan adalah 18180, maka jumlah tiga bilangan terkecil yang pertama dari bilangan-bilangan tersebut adalah ….

Pembahasan

Soal di atas adalah deret aritmetika dengan data-data sebagai berikut:

n = 101
b = 3
S101 = 18180
S3 = ?

Jumlah n suku pertama deret aritmetika dirumuskan sebagai:

Sn = ½ n[2a + (n − 1)b]
S101 = ½ × 101[2a + (101 − 1) × 3]
18180 = ½ × 101(2a + 300)
180 = ½ × (2a + 300)
180 = a + 150
a = 30

Karena suku pertama deret tersebut 30 dan bedanya 3 maka tiga suku pertama adalah:

30, 33, 36

Jumlah ketiganya adalah:

Jadi, jumlah tiga bilangan terkecil yang pertama dari bilangan-bilangan tersebut adalah 99 (E).

Simak Pembahasan 100 Soal TIU SKD CPNS 2019 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih

Semoga Bermanfaat

Related posts:

Leave a Reply

Your email address will not be published. Required fields are marked *